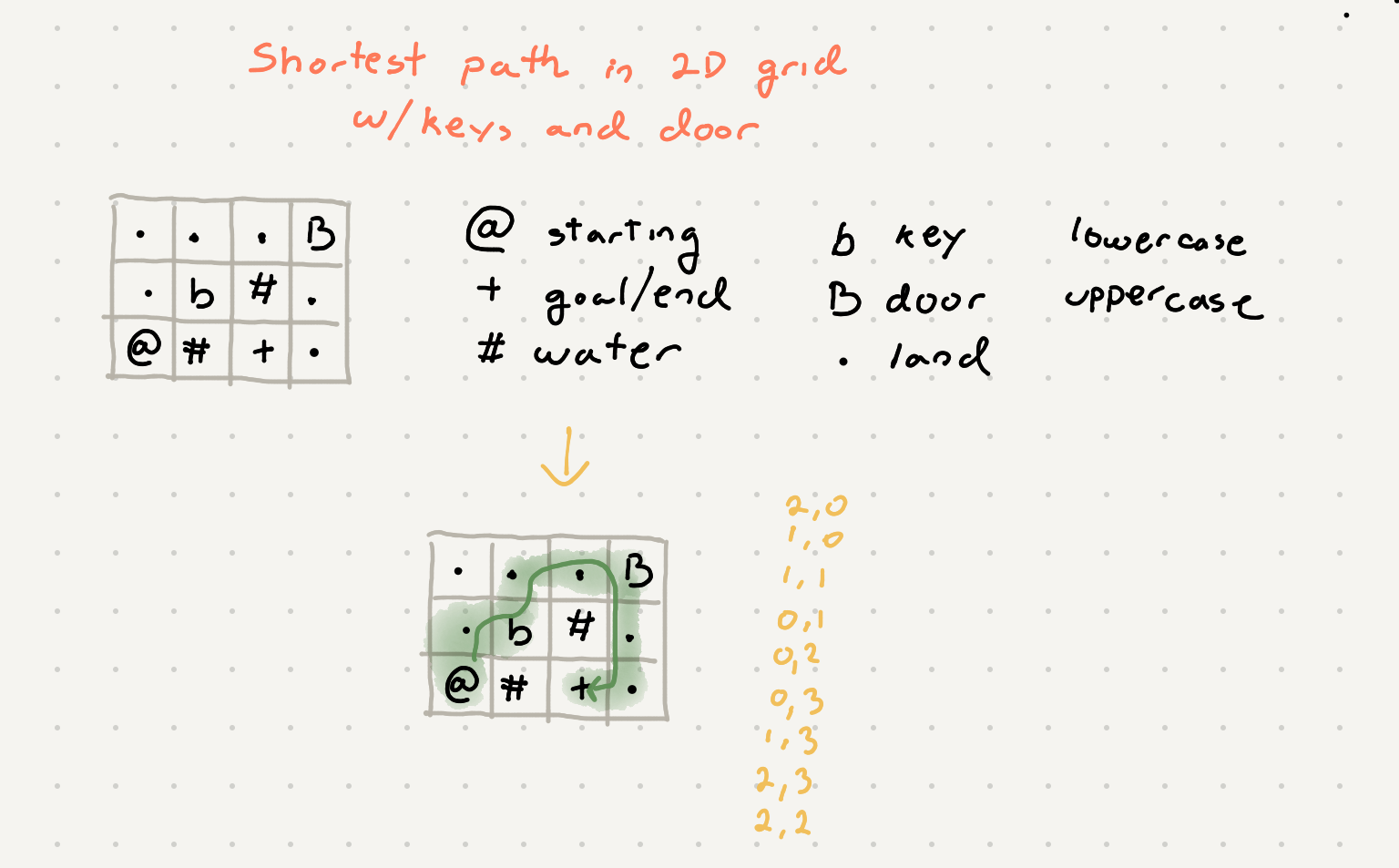
Shortest path in grid w/keys and door
Problem statement
You’re given a 2D grid that represents a maze-like area. There are some obstacles such as doors and water. You can only traverse on land and through doors that you have the key for. The goal is to find the shortest path from the start to the goal
You can go up, down, left or right from a cell, but not diagonally. Each cell in the grid can be either land or water or door or key to some doors.
There are only keys that labeled a-j. Each type of key will open only one type of door. There can be multiple identical keys of the same type. There can also be multiple doors of the same type. You cannot travel through a door, unless you have picked up the key to that door before arriving there. If you have picked up a certain type of key, then it can be re-used on multiple doors of same kind.
Given that we have a grid we can start thinking of this as a graph problem. We’ve done some graph problems have constraints in the movement such as Knights tour. We’ve also done a problem that looks at the shortest path in a grid and also returns the path Shortest path between nodes in a graph.
Let’s remind ourselves of what that code looks like -
from collections import deque
def shortest_path(start, target):
q = deque()
q.append(start)
back_ref = {} # replaces seen from normal bfs
back_ref[start.val] = None
while q:
cur = q.popleft()
if cur.val == target.val:
break
for n in cur.neighbors:
if n.val not in back_ref:
back_ref[n.val] = cur
q.append(n)
# no target found
if target.val not in back_ref:
return []
# now we take cur and go backwards
output = []
cur = target
# Will stop at the start since the
# back ref was set to None
while cur:
output.append(cur.val)
cur = back_ref[cur.val]
# reverse order
output.reverse()
return output
We will need to heavily modify this BFS approach for our problem.
Let’s discuss what kind of changes we need to make
-
We need a way to find our starting point since we’re given just the grid. We can write a straightforward
get_starting_position()as we can just write a function to scan the grid and return the start. -
We need a way to store the keys a path has picked up. The keys can only be between (a-j)
-
a
get_neighbors()function that returns the possible paths from a given point in the grid
When I first tried to solve this problem I didn’t allow the algorithm to travel to a cell that it has already visited. Now this is incorrect because we might have picked up a key that opens a path for us. That path could be the shortest path to the end. Consider the following modified grid with additional door and key -
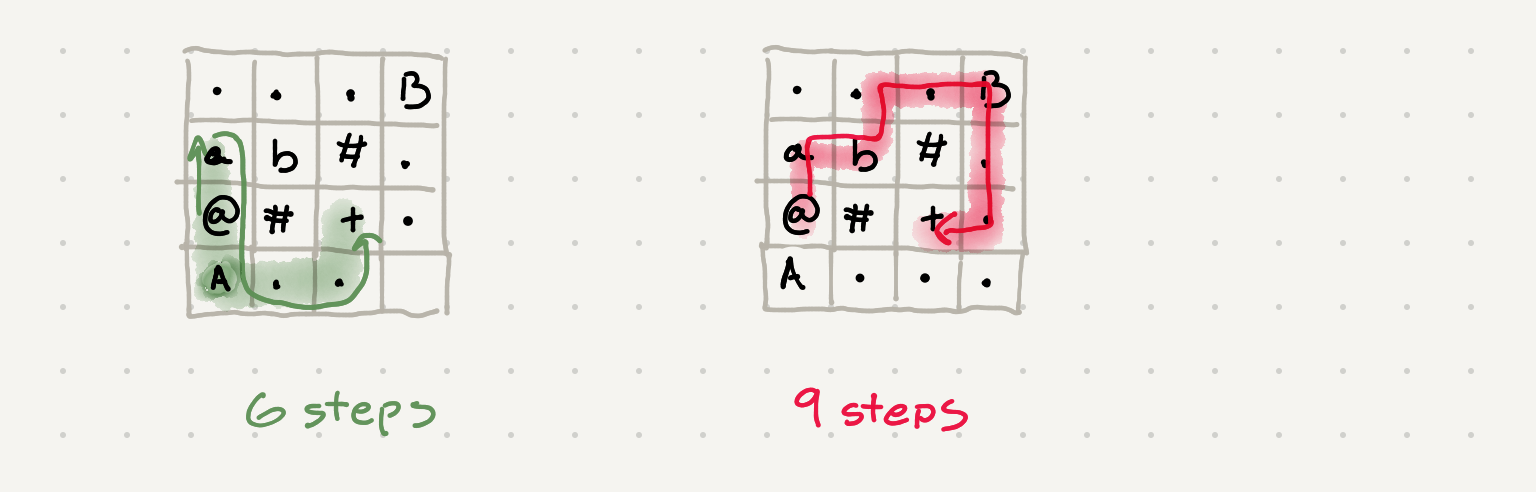
You can see that a standard BFS that doesn’t allow us to revisit cells will yield us the wrong result. So how do we allow us to revisit cells but also prevent ourselves from causing an infinite loop or traversal?
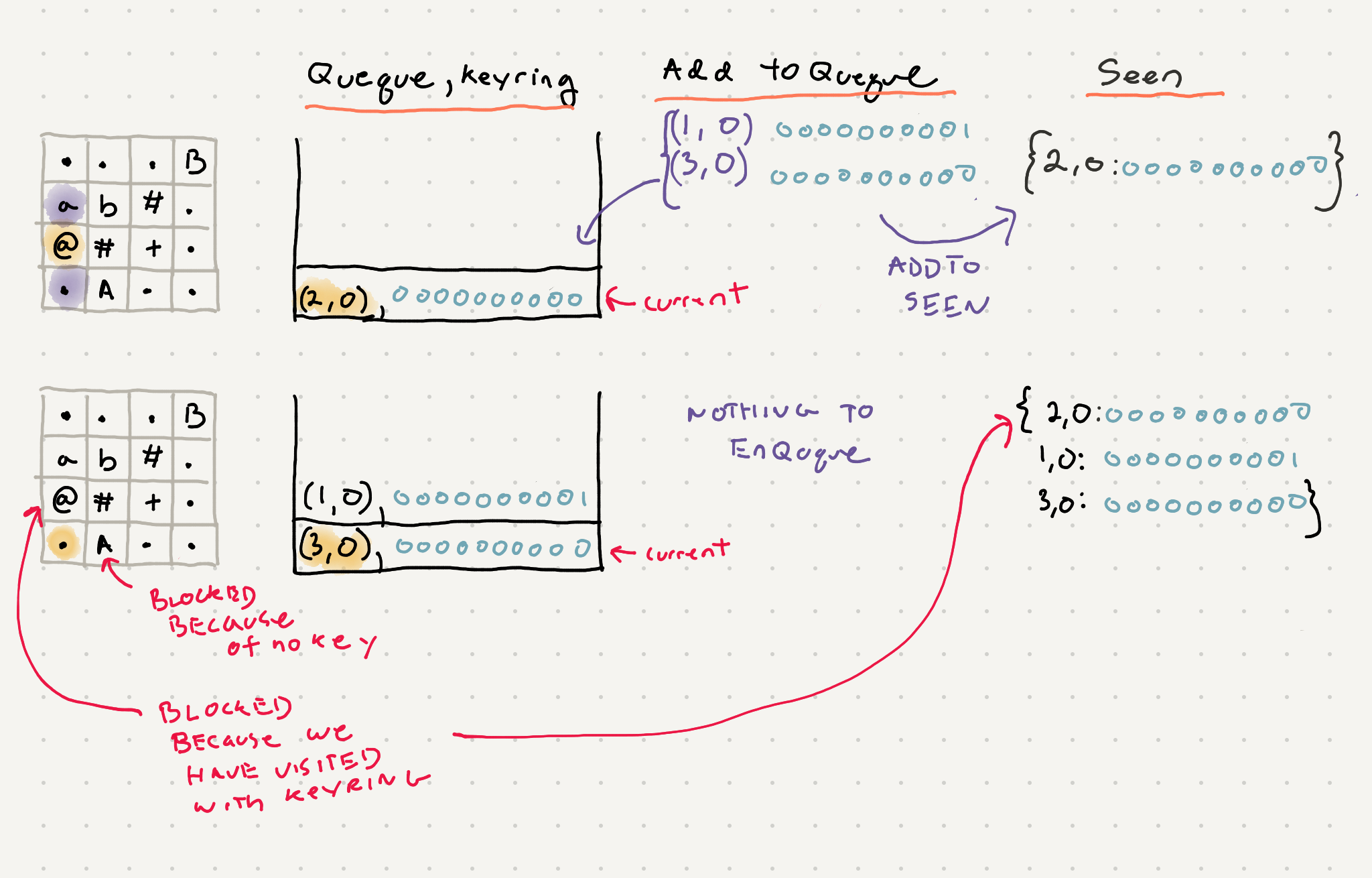
One possible solution is to not just track the visited cells but also the keys in your possession at the time of traversal. This way if we are visiting a cell with a new set of keys we are allowed to visit it but if we’ve traveled this cell with the same set of keys we can stop traversing.
So how exactly do we store the key_ring (the container that houses all the paths keys)?
A list is mutable in python so it cannot be hashed. We could store a tuple with 10 values each representing one of the 10 keys available. But instead of doing with with 10 int values we can use a 10 bit integer and assume each bit represents 1 key. Let’s take a look

So now that we have a new key we also need to keep track of our visited nodes in a different way. We can use a dictionary with the position of the node as the key and a set of all key_rings as the value. Putting it together the traversal would look like this:
Notice how the path south from the starting position is blocked because we don’t have the key to open door A
But once we explore the path that picks up the A key and we modified our bfs we can traverse back down south
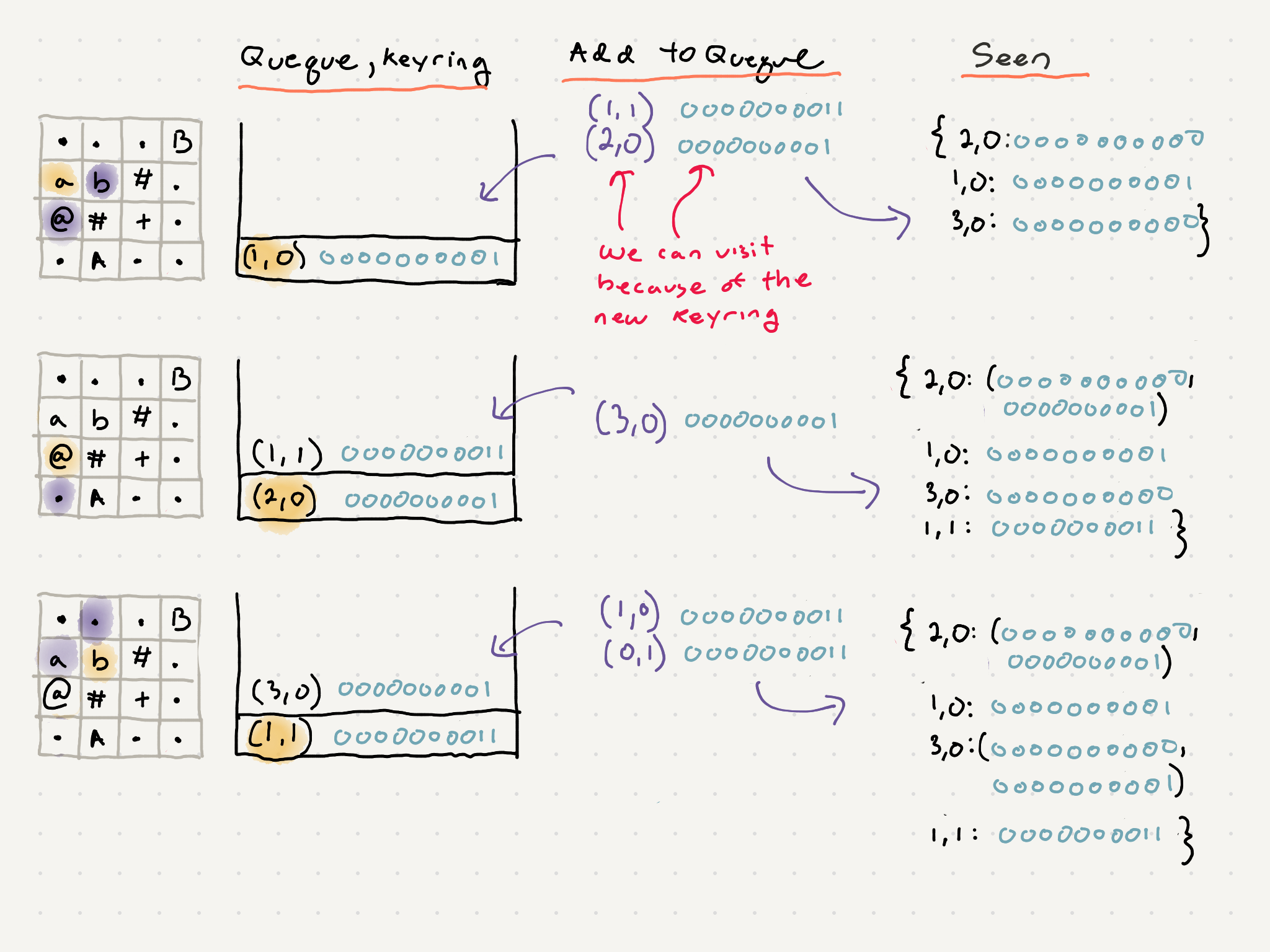
Because we keep track of key_rings and positions visited we can stop ourselves from going back north to the starting position
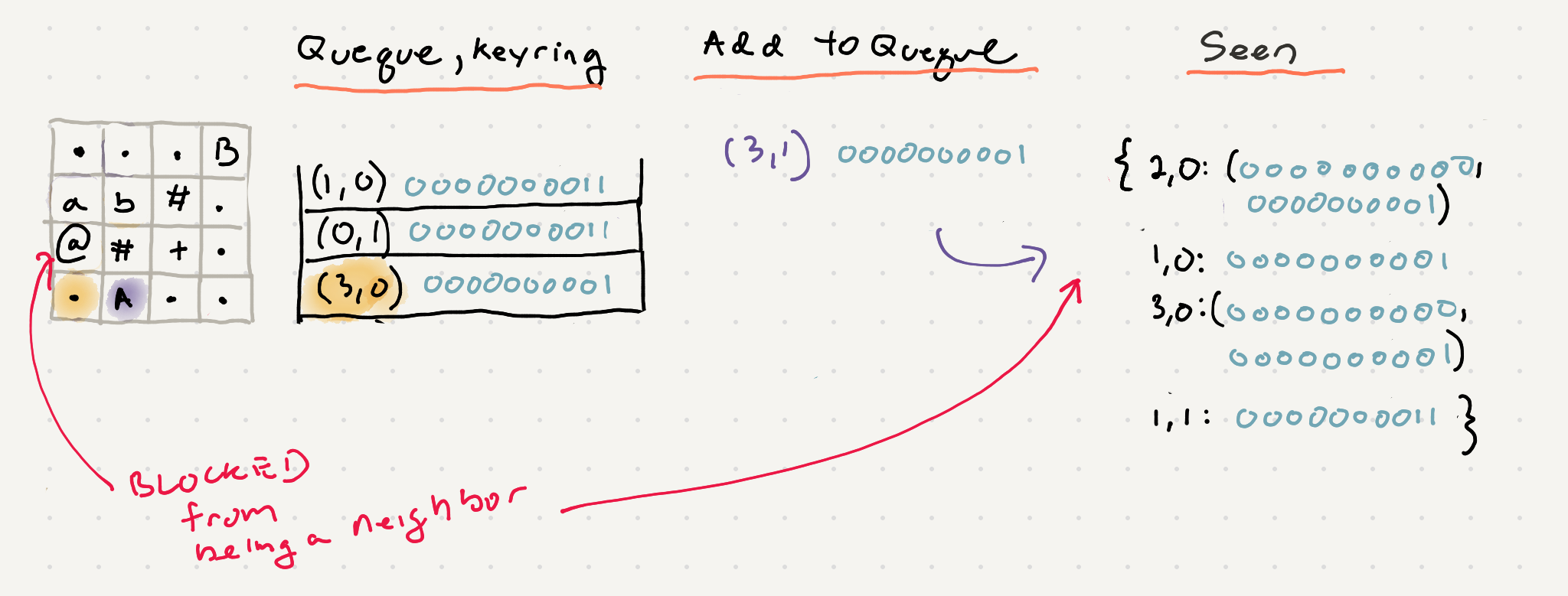
So during the traversals we see we need a few helper functions to block the enqueing of visited cells with the same key ring. We can write a helper function is_visited() to help with this.
def is_visited(new_row, new_col, new_key_ring, seen):
for key in seen[(new_row, new_col)]:
if new_key_ring == key:
return True
return False
So we have a way of efficiently storing the key locations but how do we actually find out if we have a key to a door when we get to it? We can use some bitwise operations and bit masks do do this. Recall each bit represents weather you have the key for a certain letter. So we need a way to look up the value at a certain bit index in our key ring. We can apply a technique called bit masking to do just this.
A mask defines which bits you want to keep, and which bits you want to clear. Masking is the act of applying a mask to a value.
If we AND / & our key ring with a binary number with only the bit we are looking for filled we will extract a subset of the bits in the value.
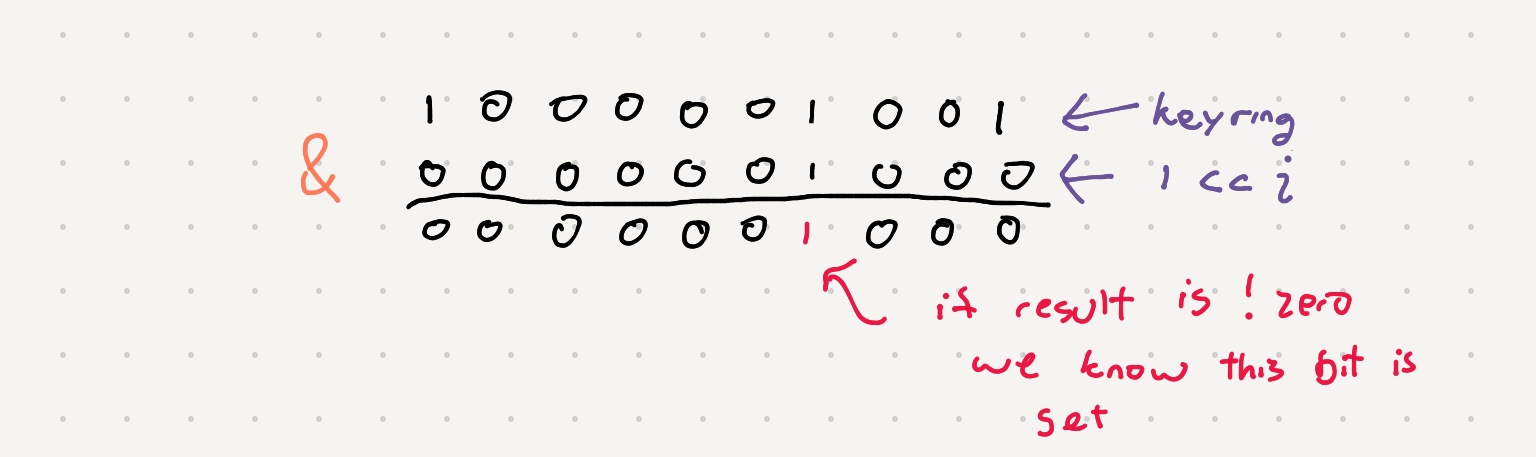
And how do we generate the mask value to apply to our key ring? We need to figure out which bit to look at when we approach a door. If you assume the letter A is the 0th position of the key ring than we can “subtract” A from the letter of the current door.
For example if we hit the letter D we want to look up the 3rd bit (0 based indexing)
ABCD
^ ^
0 |
|
3
We see that D should be 3 positions away from A. You can’t subtract strings in python but you can subtract the ordinal value of these letters. The ordinal value is going to return the ASCII value of that string
>>> ord('A')
65
>>> ord('D')
68
>>> ord('D') - ord('A')
3

Once we have the position we can take the number 1 or 0000000001 in binary and shift that bit in the 0th index 3 times
>>> 1 << 3
8
>>> "{0:b}".format(8)
'1000'
In summary we need:
- Find the positions of the bit/door you want to look up (
ord('LETTER TO LOOK UP') - ord('A')) - Left shift that position to 1 (
0000000001) (1 << i) - And the key ring and the result of step 2 (
key_ring & 1 << i) - If the result is 0 we know that bit is unset and we don’t have the key for that door. Else we do and we can proceed
The final formula looks like this
if key_ring & (1 << (ord(door_to_lookup) - ord('A'))) == 0:
# don't have access to door
Let’s summarizes as well all our different neighbor situations
| cell type | action |
|---|---|
| water | don’t include |
| locked door | don’t include |
| door w/key | include |
| land | include |
| door or land w/keyring already seen | don’t include |
Putting it all together
from collections import deque
STOP_POSITION = '+'
START_POSITION = '@'
WATER = '#'
def find_shortest_path(grid):
row_length = len(grid)
col_length = len(grid[0])
start_row, start_col = find_starting_position(grid, row_length, col_length)
# we need this variables to build the path from our backref object
stop_row, stop_col, stop_key_ring = False, False, False
# initialize all values of the grid with empty sets in the dictionary
seen = {(row, col):set() for row in range(row_length) for col in range(col_length)}
seen[(start_row, start_col)].add(0)
# we will use this to rebuild the shortest path
backref = {(start_row, start_col, 0): None}
# add the starting point and starting keyring into the queue and seen objects
q = deque()
q.append((start_row, start_col, 0))
while q:
cur_row, cur_col, key_ring = q.popleft()
# We found the node we are looking for
if grid[cur_row][cur_col] == STOP_POSITION:
stop_row, stop_col, stop_key_ring = cur_row, cur_col, key_ring
break
for new_row, new_col, new_key_ring in get_neighbors(grid, cur_row, cur_col, key_ring):
if not is_visited(new_row, new_col, new_key_ring, seen):
q.append((new_row, new_col, new_key_ring))
backref[(new_row, new_col, new_key_ring)] = cur_row, cur_col, key_ring
seen[(new_row, new_col)].add(new_key_ring)
path = []
if all([stop_row, stop_col, stop_key_ring]):
current = stop_row, stop_col, stop_key_ring
while current:
row, column, key_ring = current
path.append((row, column))
current = backref[current]
path.reverse()
return path
def find_starting_position(grid, row_length, col_length):
r, c = None, None
for i in range(row_length):
for j in range(col_length):
if grid[i][j] == START_POSITION:
r, c = i,j
break
return r, c
def is_visited(new_row, new_col, new_key_ring, seen):
for key in seen[(new_row, new_col)]:
if new_key_ring == key:
return True
return False
def get_neighbors(grid, row, col, key_ring):
DIRECTIONS = [[0, 1], [1, 0], [0, -1], [-1, 0]]
row_length = len(grid)
col_length = len(grid[0])
available_neighbors =[]
for direction_row, direction_col in DIRECTIONS:
new_row, new_col = row + direction_row, col + direction_col
if not (0 <= new_row < row_length and 0 <= new_col < col_length):
continue
pos_val = grid[new_row][new_col]
if pos_val == WATER:
continue
if pos_val in 'ABCDEFGHIJ' :
if key_ring & (1 << (ord(pos_val) - ord('A'))) == 0:
continue
if pos_val in 'abcdefghij':
# we found a key. Let's make sure it's in our keyring
new_key_ring = key_ring | (1 << (ord(pos_val) - ord('a')))
else:
new_key_ring = key_ring
available_neighbors.append((new_row, new_col, new_key_ring))
return available_neighbors