Shortest path between nodes in a graph

Problem statement

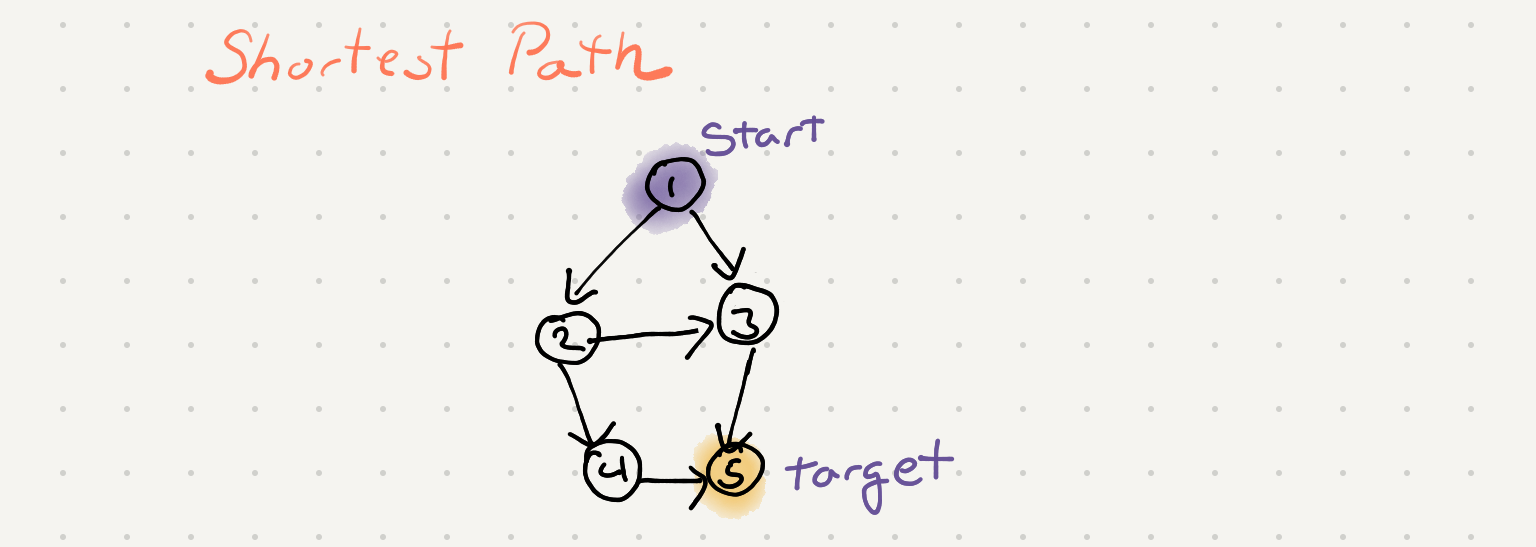
Given a unweighted graph, a source and a destination, find the shortest path from source to destination in the graph

problem

Before we start this problem let’s take a quick look on how we would traverse a graph. In this case we can use a Bread first approach so we can determine the shortest distance.

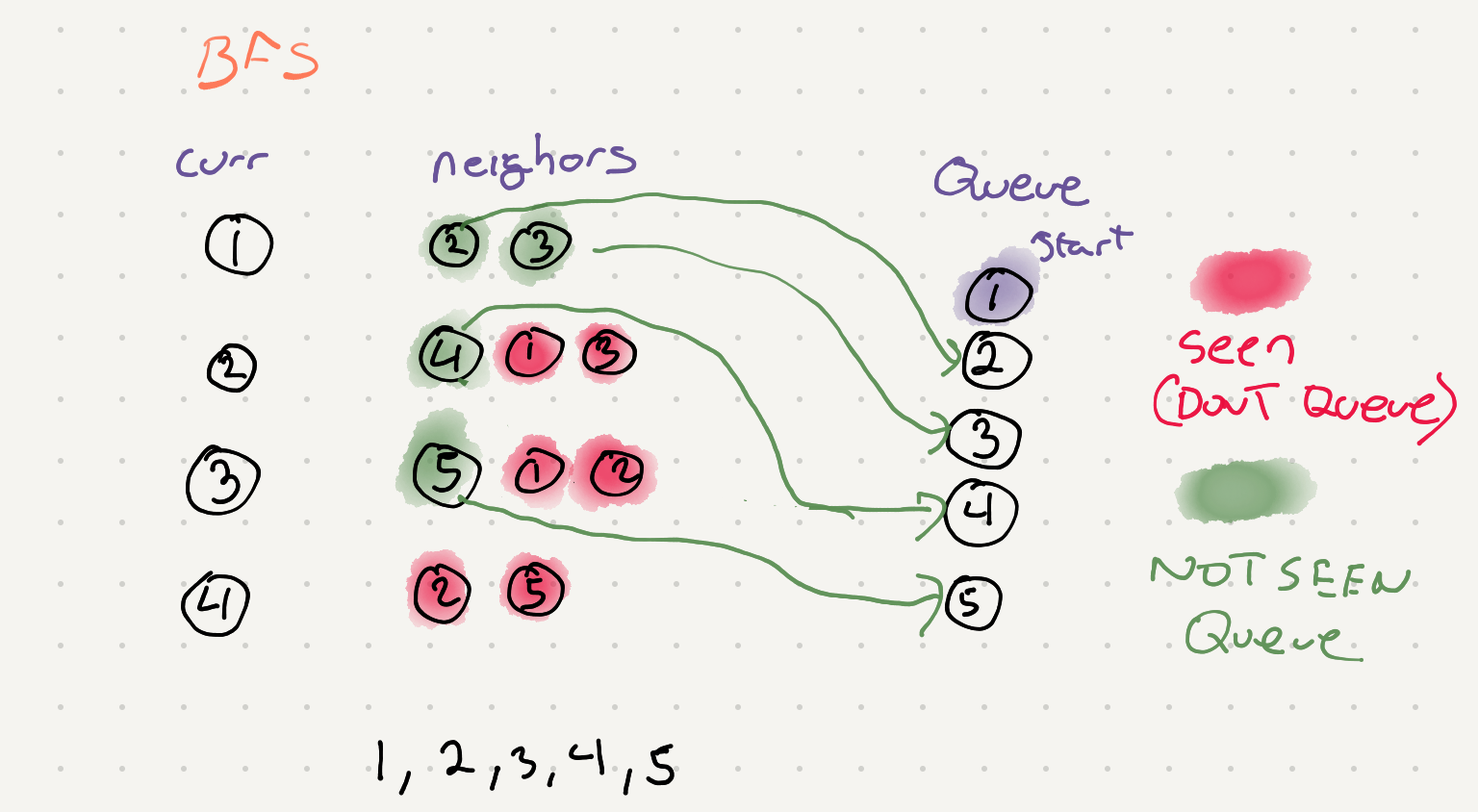
problem

def bfs(start):
    visited = set()
    q = deque()
    q.append(start)

    visited.append(start.val)

    while q:
        cur = q.popleft() # fifo
        print(cur.data)

        for n in cur.neighbors:
            if (n.val not in visited):
                q.append(n)
                visted.append(n.val)

Now that we know how to traverse lets try to figure out how to find a specific node and also the shortest path. Consider the following graph. Lets say we want to get to Node(5) from Node(1). We see there are a few different paths but only 1 that is 2 hops away. We can modify our existing bfs code to do a check for the cur.val == target.val and find the node we’re looking for but that doesn’t give us a way to get the path back to the starting point. To do that we can save the previous connected node for the current node. This way we can traverse back to the start similar to a linked list.

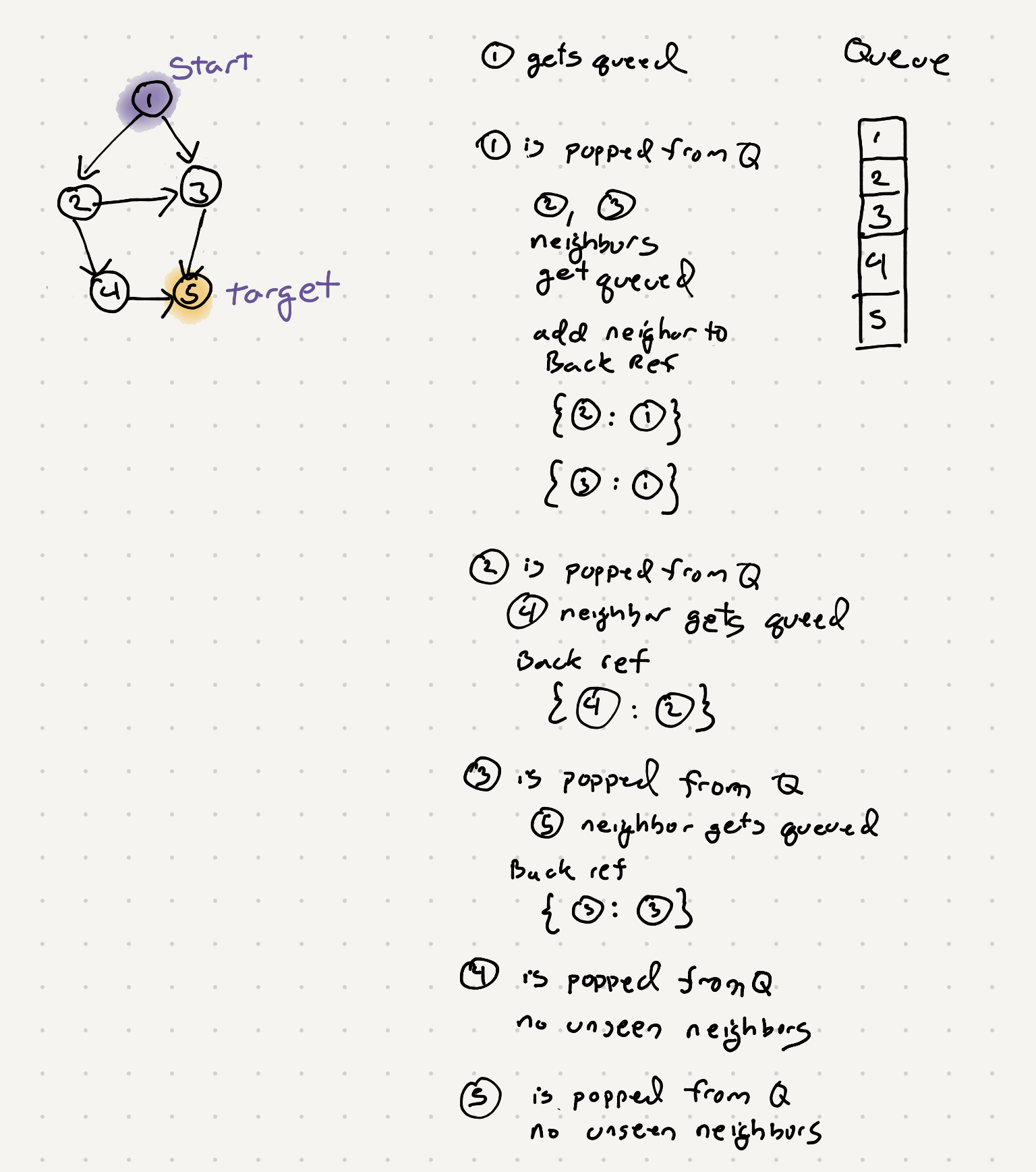
problem

Once we have a dictionary of back references we can iterate through from the cur value while looking up values

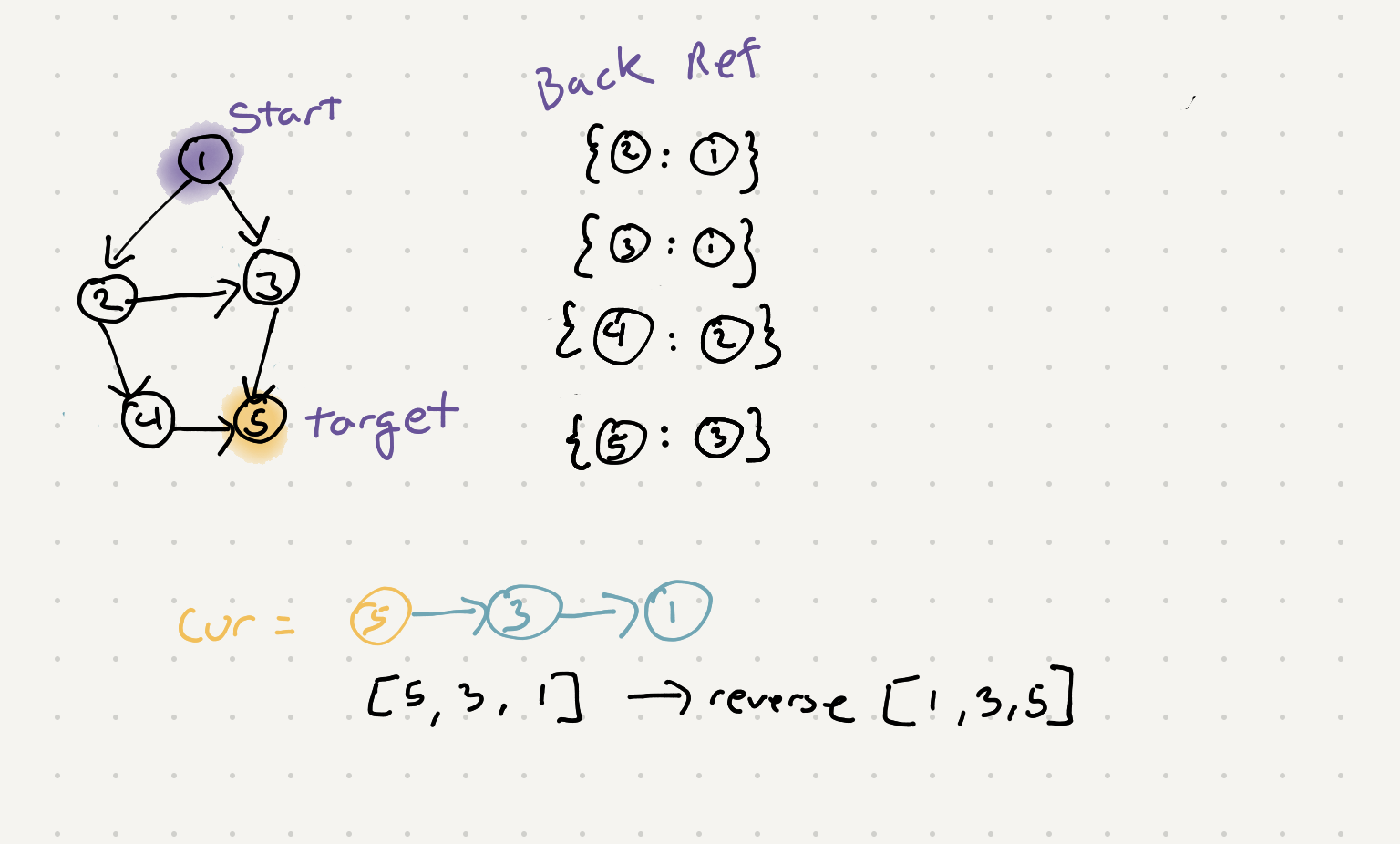
problem

Putting it all together -

from collections import deque

def shortest_path(start, target):
    q = deque()
    q.append(start)
    back_ref = {}   # replaces seen from normal bfs
    back_ref[start.val] = None

    while q:
        cur = q.popleft()
        if cur.val == target.val:
            break

        for n in cur.neighbors:
            if n.val not in back_ref:
                back_ref[n.val] = cur
                q.append(n)

    # no target found
    if target.val not in back_ref:
        return []

    # now we take cur and go backwards
    output = []
    cur = target

    # Will stop at the start since the
    # back ref was set to None
    while cur:
        output.append(cur.val)
        cur = back_ref[cur.val]

    # reverse order
    output.reverse()
    return output