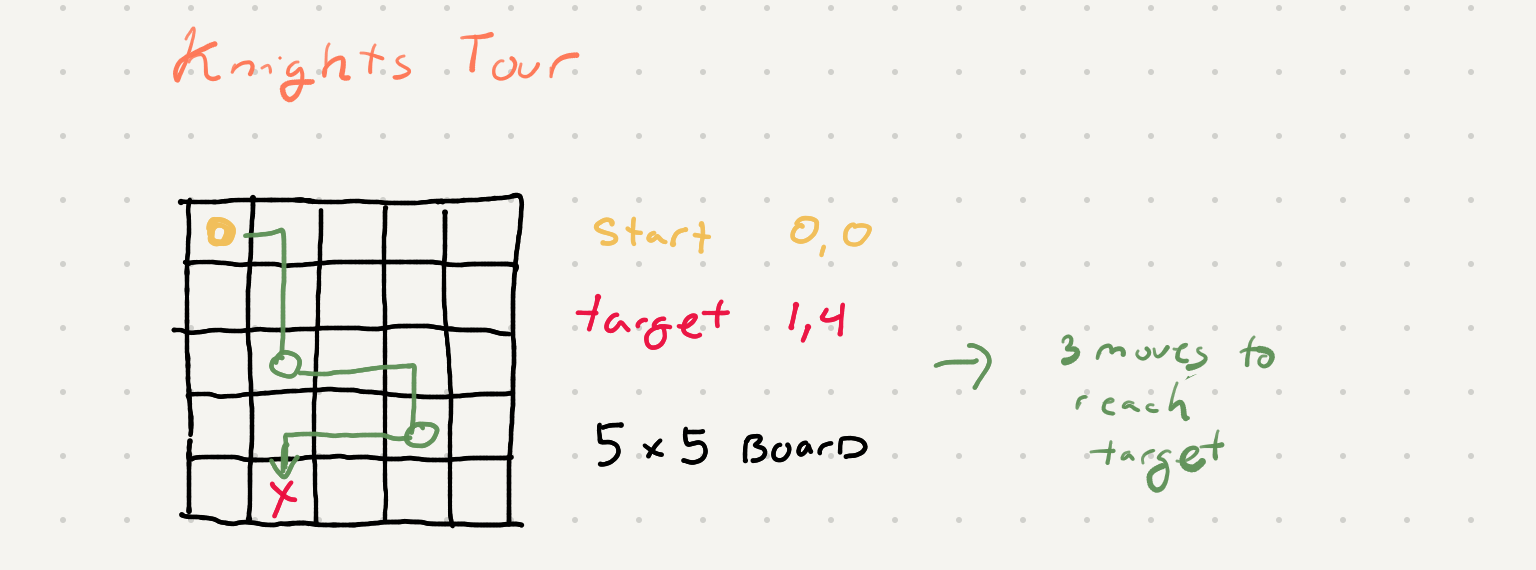
Knights tour on a chess board

Problem Statement:

You are given a rows * cols chessboard and a knight that moves like in normal chess. Currently knight is at starting position denoted by start_row th row and start_col th col, and want to reach at ending position denoted by end_row th row and end_col th col.
The goal is to calculate the minimum number of moves that the knight needs to take to get from starting position to ending position.

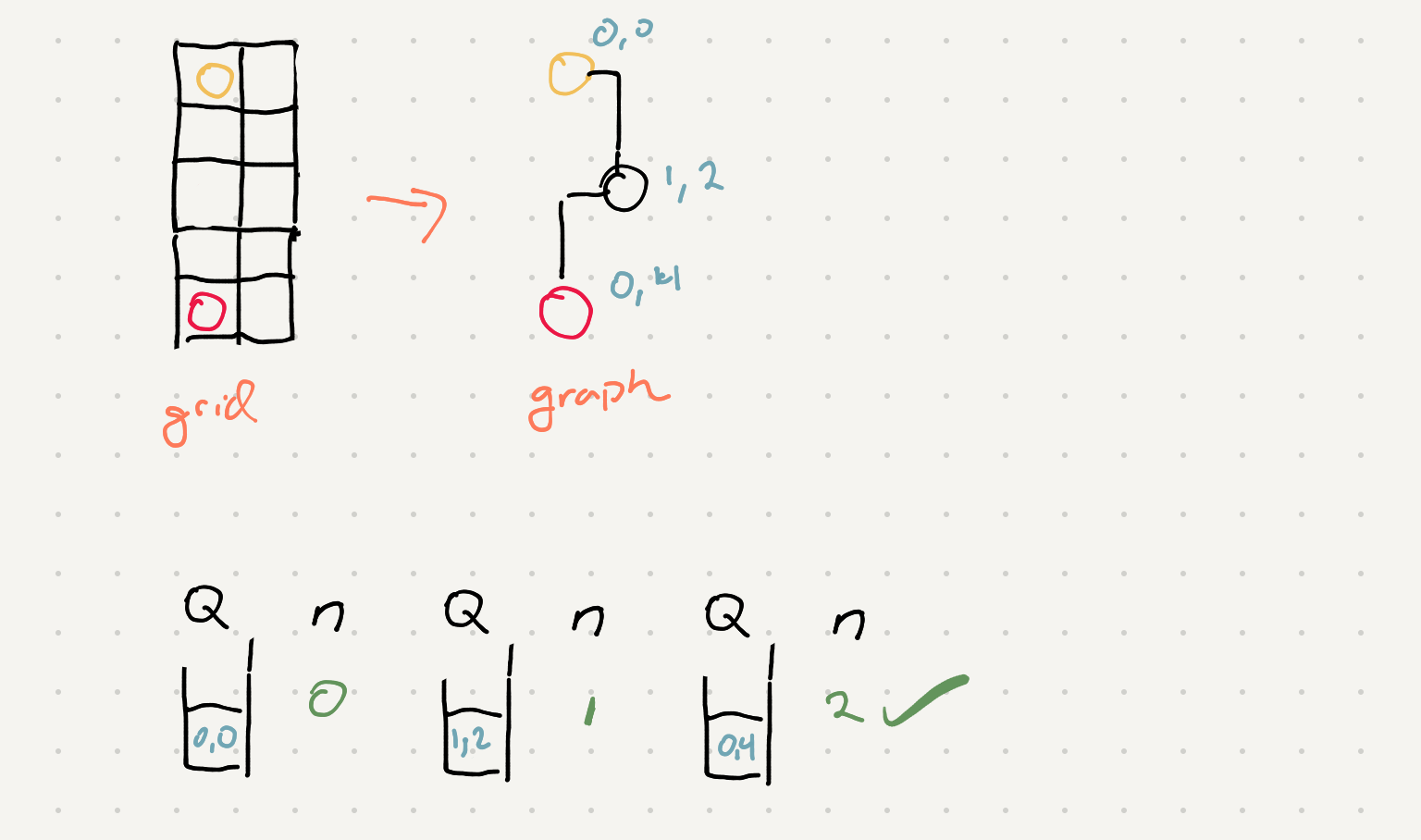
A knight in chess has a specific pattern of movements. Let’s plot out the ways a knight could move if we were in a grid

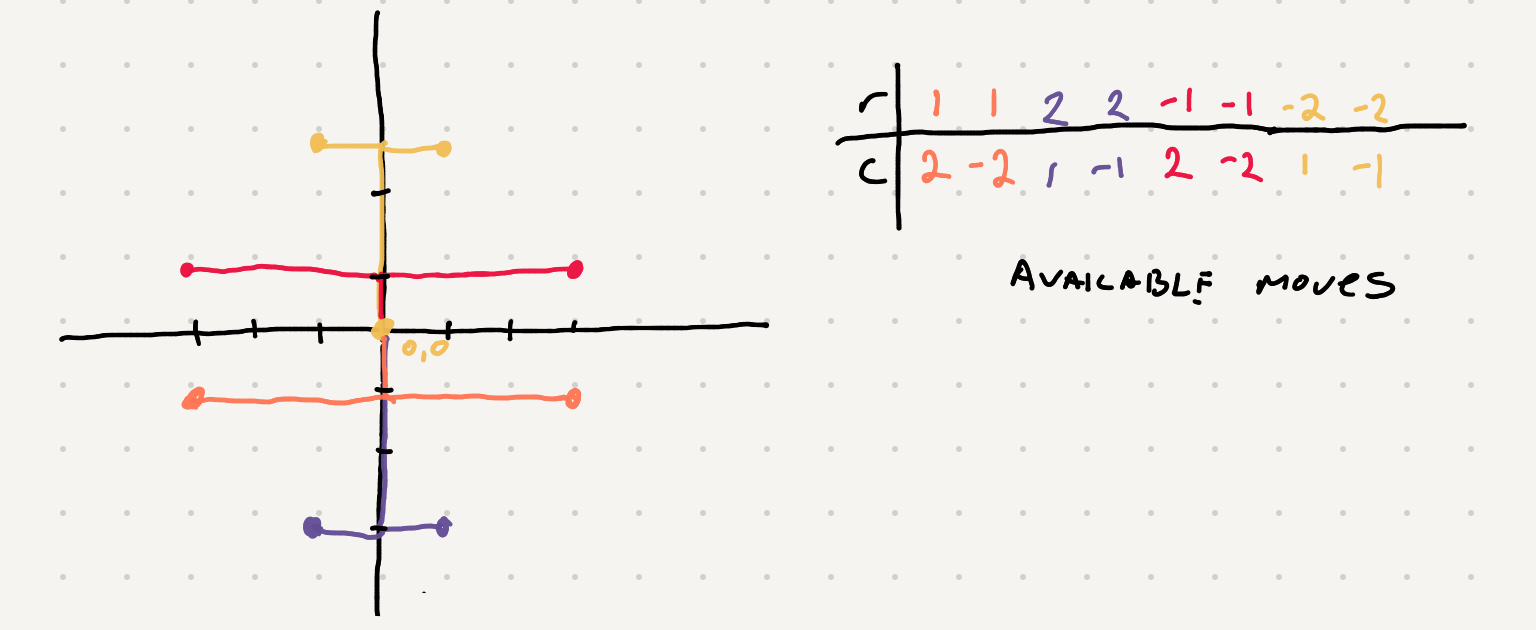
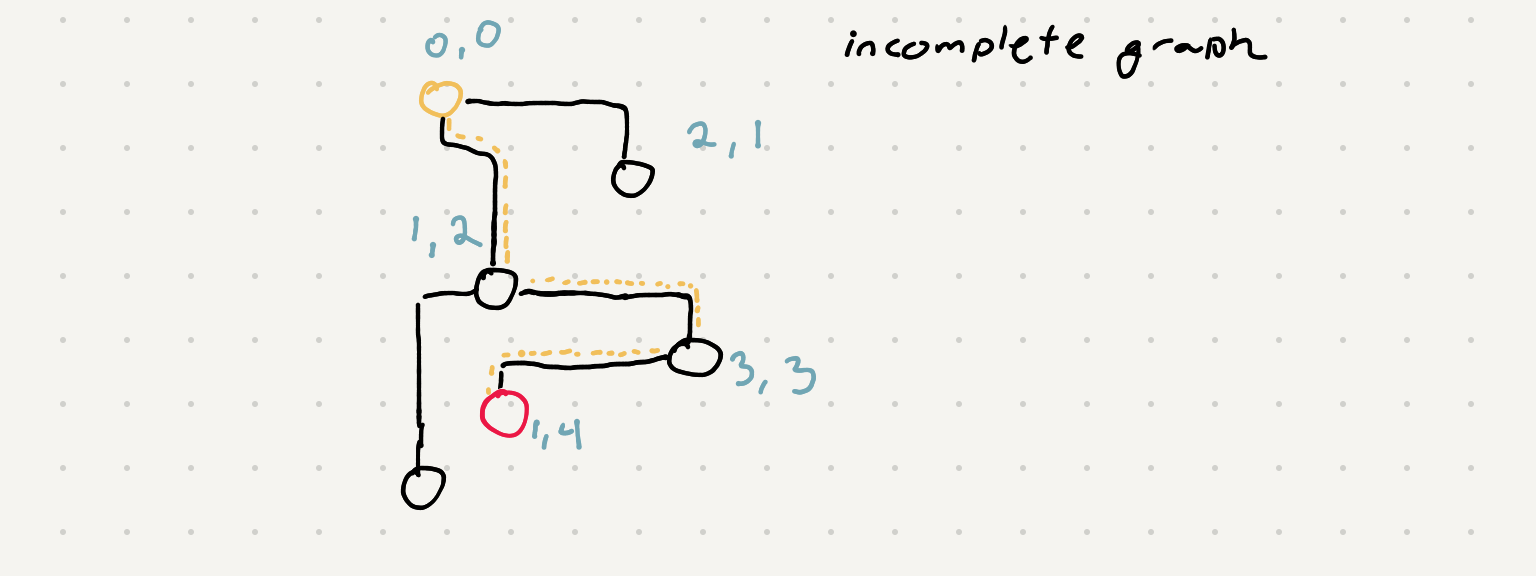
One way to approach this problem is to treat the available positions from a box in the chessboard to another box as a graph. All the valid movement slots are a nodes neighbors.

Given that we have to find the shortest number of hops to the target a bfs approach seems appropriate here. Here is a quick reminder of the bfs algo.

def bfs(start):
    visited = set()
    q = deque()
    q.append(start)

    visited.append(start.val)

    while q:
        cur = q.popleft() # fifo
        print(cur.data)

        for n in cur.neighbors:
            if (n.val not in visited):
                q.append(n)
                visted.append(n.val)

So we need a couple of modifications to the bfs algo for our original problem

1. a way to get neighbors
2. a way to keep track of the number of moves
3. a way to know when we hit our target

For our neighbors we have 8 available moves but not all of them might be valid (ie might be out of the board)

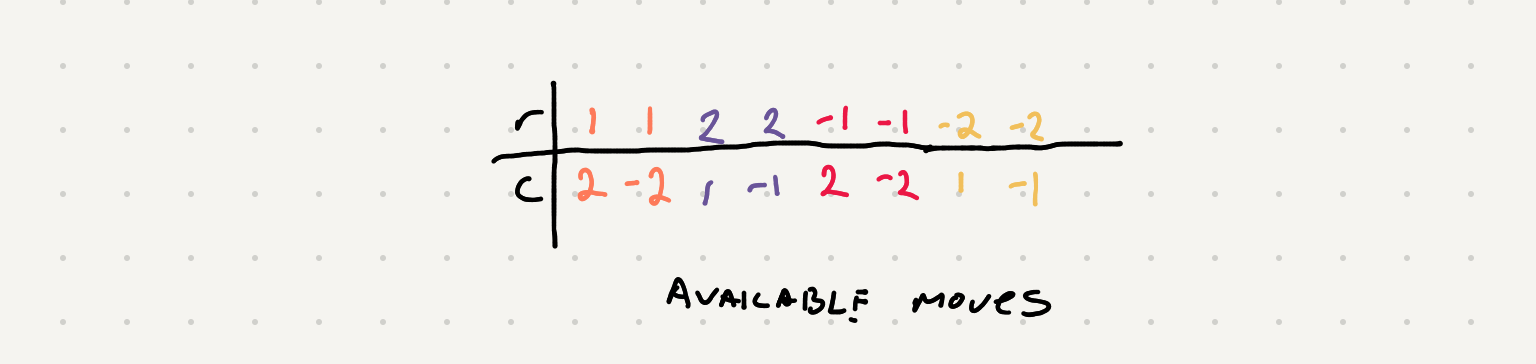
we can have a check that checks the new positions against the grid size

0 <= new_row < num_of_rows and 0 <= new_col < num_of_cols

For keeping track of the number of moves we can enqueue the number of moves into the queue as well and increment it when a new neighbor gets processed

Putting it all together

from collections import deque

DIRECTIONS = [(2, 1), (2, -1), (-2, 1), (-2, -1), (1, 2), (1, -2), (-1, 2), (-1, -2)]

def find_minimum_number_of_moves(num_row, num_col, start_r, start_c, target_r, target_c):
    def get_neighbors(r, c):
        neighbors = []
        for direction_r, direction_c in DIRECTIONS:
            new_r, new_c = r + direction_r, c + direction_c
            if 0 <= new_r < num_row and 0 <= new_c < num_col:
                neighbors.append((new_r, new_c))

        return neighbors	

    visited = set()
    
    q = deque()
    q.append(((start_r, start_c), 0))
    visited.add((start_r, start_c))
    
    while q:
        cell, count = q.popleft() # fifo
        if (cell[0], cell[1]) == (target_r, target_c):
            return count
    
        for new_r, new_c in get_neighbors(cell[0], cell[1]):
            if ((new_r, new_c) not in visited):
                q.append(((new_r, new_c), count + 1))
                visited.add((new_r, new_c))

    return -1

Time complexity will be O(n) where n is number of items in the grid (r * c)