Quicksort - Dutch national flag

Problem Statement:

Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue. Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.
Could you come up with a one-pass algorithm using only constant space?

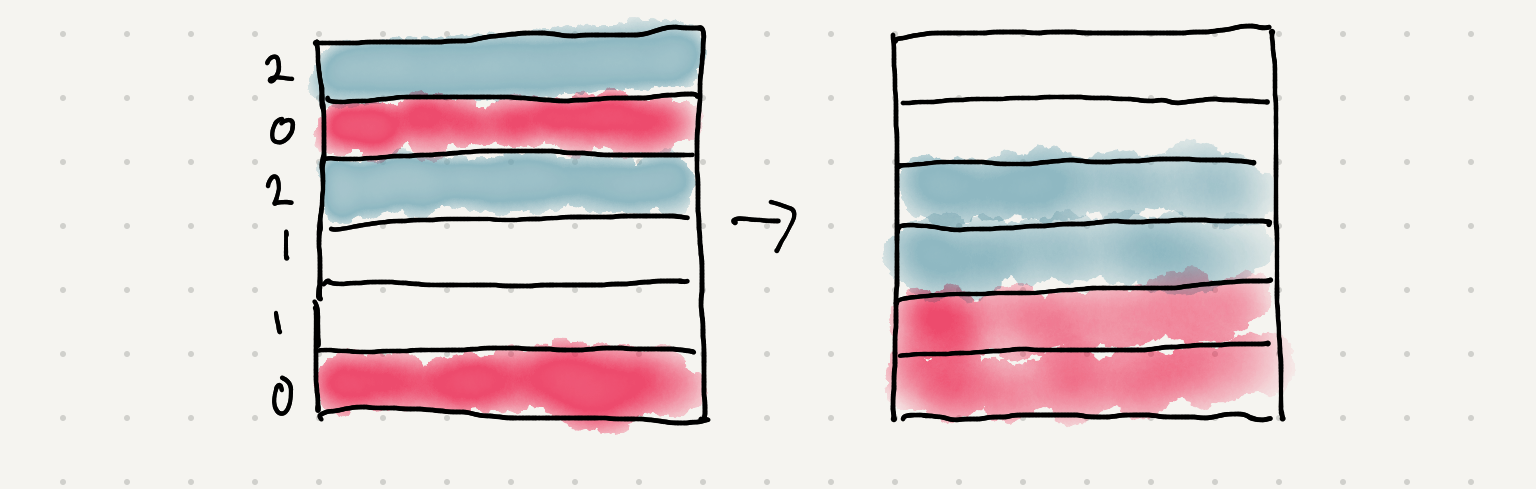
problem

So the easier solution would involve iterating through the original array and count the number of colored objects and just overwriting the original array in a second pass.

To be able to solve this problem I’d recommend brushing up on quicksort. If you recall the partition step of quicksort has some interesting effects. It puts all the smaller elements of the pivot to the left and all elements larger to the right.

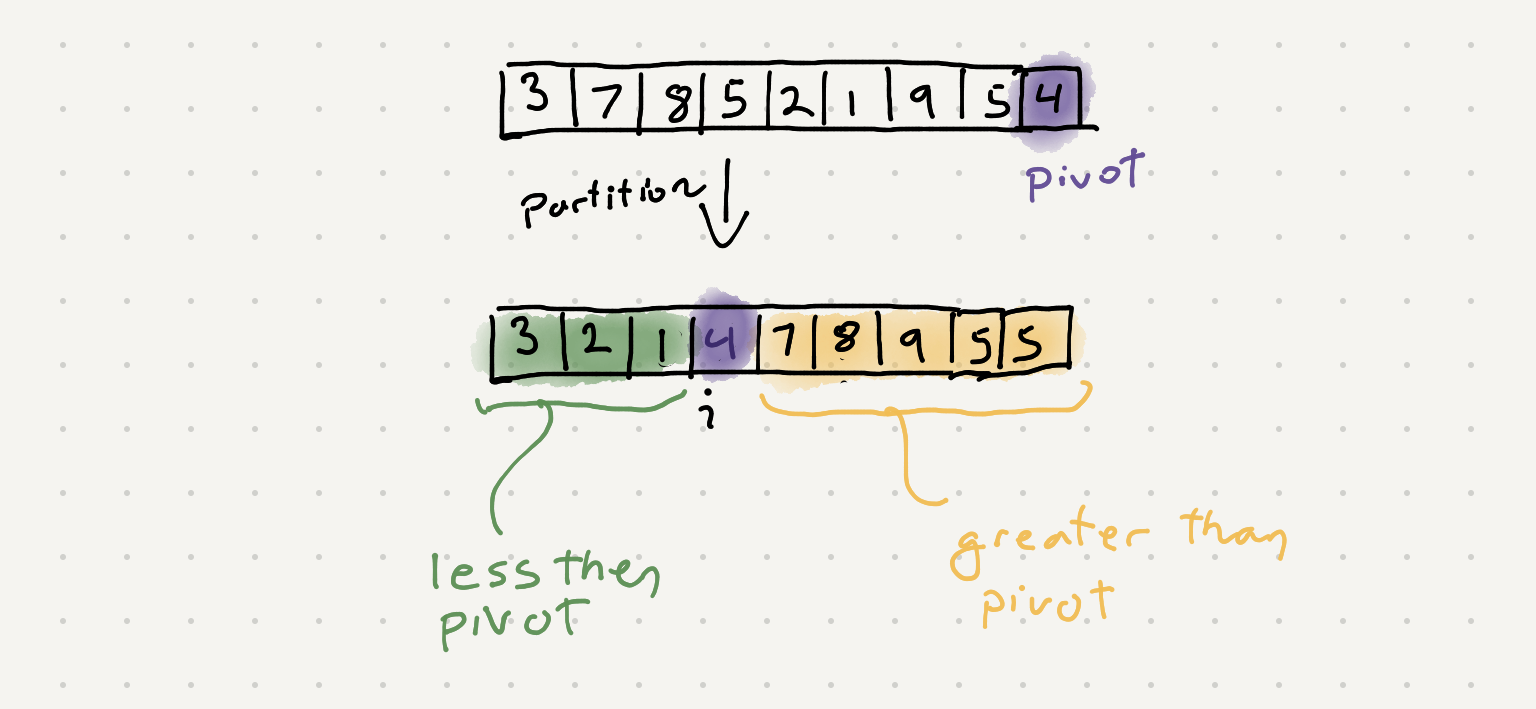
pivot

Using this idea we can solve this problem with 2 passes O(~2N) time complexity and O(1) space.

RED = 0
WHITE = 1
BLUE = 2

def sortColors(nums: List[int]) -> None:
    # first pass organize all red
    end_of_red = 0
    
    for x in range(len(nums)):
        if nums[x] == RED:
            nums[end_of_red], nums[x] = nums[x], nums[end_of_red]
            end_of_red += 1
            

    # second pass organize all white
    start_of_white = end_of_red
    
    for x in range(start_of_white, len(nums)): 
        if nums[x] == WHITE:
            nums[start_of_white], nums[x] = nums[x], nums[start_of_white]
            start_of_white += 1

Let’s try to modify that partition function to organize our colors in one pass. Since we are really only sorting 3 numbers/colors we can keep track of where we’re inserting red objects in the front and where we are inserting blue objects in the back.

example

RED = 0
WHITE = 1
BLUE = 2

def sortColors(nums: List[int]) -> None:
    p1 = 0                  # end of red colors
    curr = 0                
    p2 = len(nums) - 1      # start of blue colors

    while curr <= p2:
        if nums[curr] == RED:
            # swap curr and p1 and move p1 forward
            nums[curr], nums[p1] = nums[p1], nums[curr]
            p1 += 1
            curr += 1
        elif nums[curr] == BLUE:
            # swap curr and p2 and move p2 back
            nums[curr], nums[p2] = nums[p2], nums[curr]
            p2 -= 1
        else:   
            curr += 1