Using two heaps to keep running list of medians
Tags:
heaps
Let’s say you wanted to compute the running median of a steam of numbers. A brute force solution would be to store all the elements and regularly sort it. This would have a time comlexity of O(n^2)
We can achieve a O(logn) runtime by maintaining two heaps, a max heap and a min heap. One of the heaps will have an extra value. If we have seen odd numbers we just take that extra value that is sorted in the max heap. If it is even we take the max from the max heap and the min from the min heap and calculate the medium
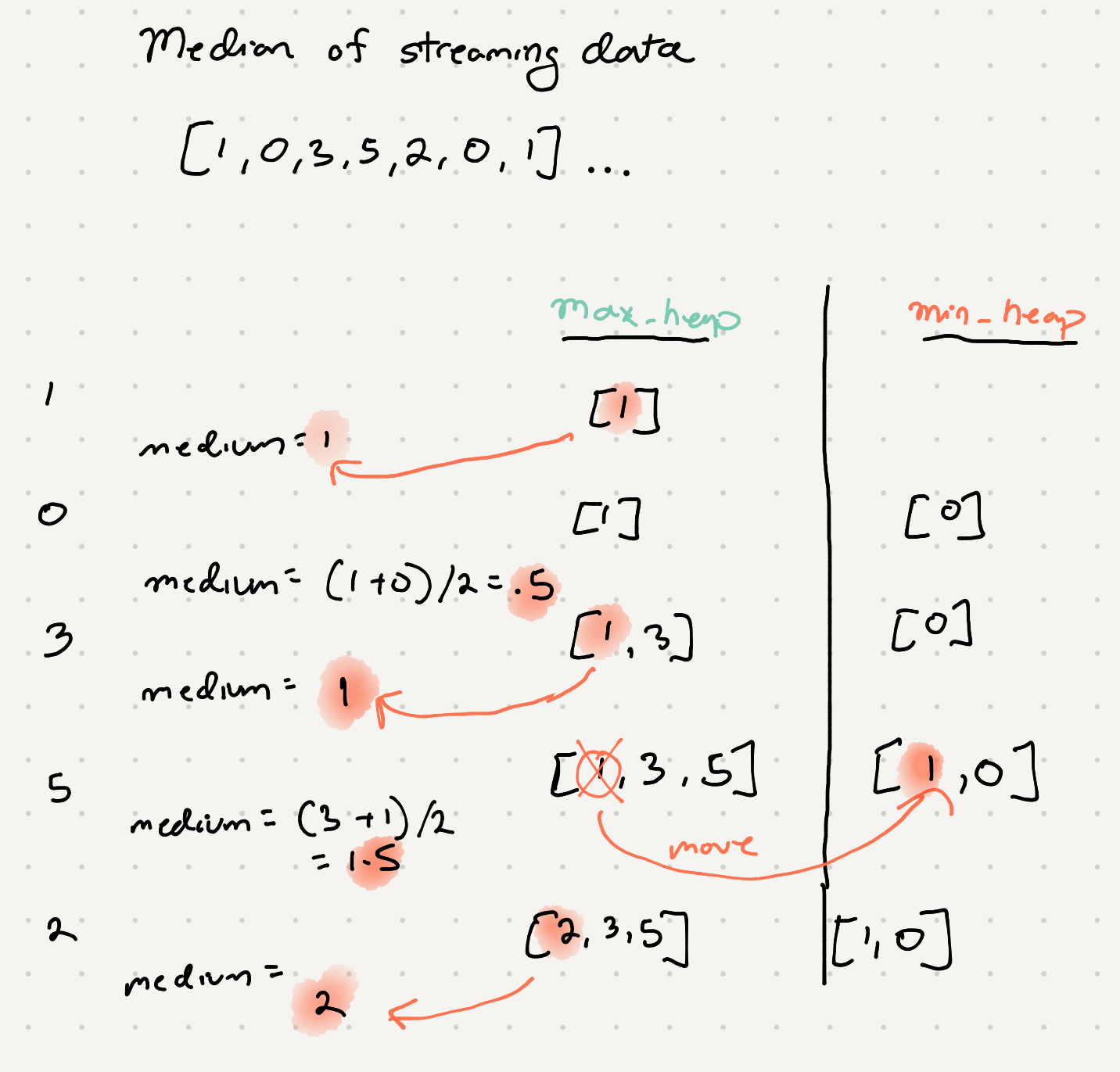
Putting it together in code
import heapq
def running_medium(streaming_list):
max_heap = [] # store smallest -> midpoint
min_heap = [] # midpoint -> largest
result = []
for num in streaming_list:
largest_from_min_heap = heapq.heappop(min_heap)
if num < largest_from_min_heap:
heapq.heappush(max_heap, num)
heapq.heappush(min_heap, largest_from_min_heap)
else:
heapq.heappush(min_heap, num)
# max heap using negative because python doesn't support it natively
heapq.heappush(max_heap, -largest_from_min_heap)
if len(max_heap) > len(min_heap):
heapq.heappush(min_heap, -heapq.heappop(max_heap))
if len(min_heap) == len(max_heap):
result.append(min_heap[0] + (-max_heap[0]) * .5)
else:
result.append(min_heap[0])
return result