Merge sorted files

Let’s say we want to write a program that takes a input of sorted sequences and computes the union of these sequences as a sorted sequence. For example for input [(3,5,7), (0,6), (0,6,28)]:

The output would be [0,0,3,5,6,6,7,28]

A brute force solution would involved combining all the sub lists and running a o(nlogn) sorting algorithm assuming n items. One thing we can do is utilize the fact that all these sub lists are sorted. If we maintain a min heap to keep the smallest number seen we can pop off the smallest element to populate the final list as we parse the sub lists

So let’s first seed our min heap with the first elements of each sub lists to get an initial sorting.

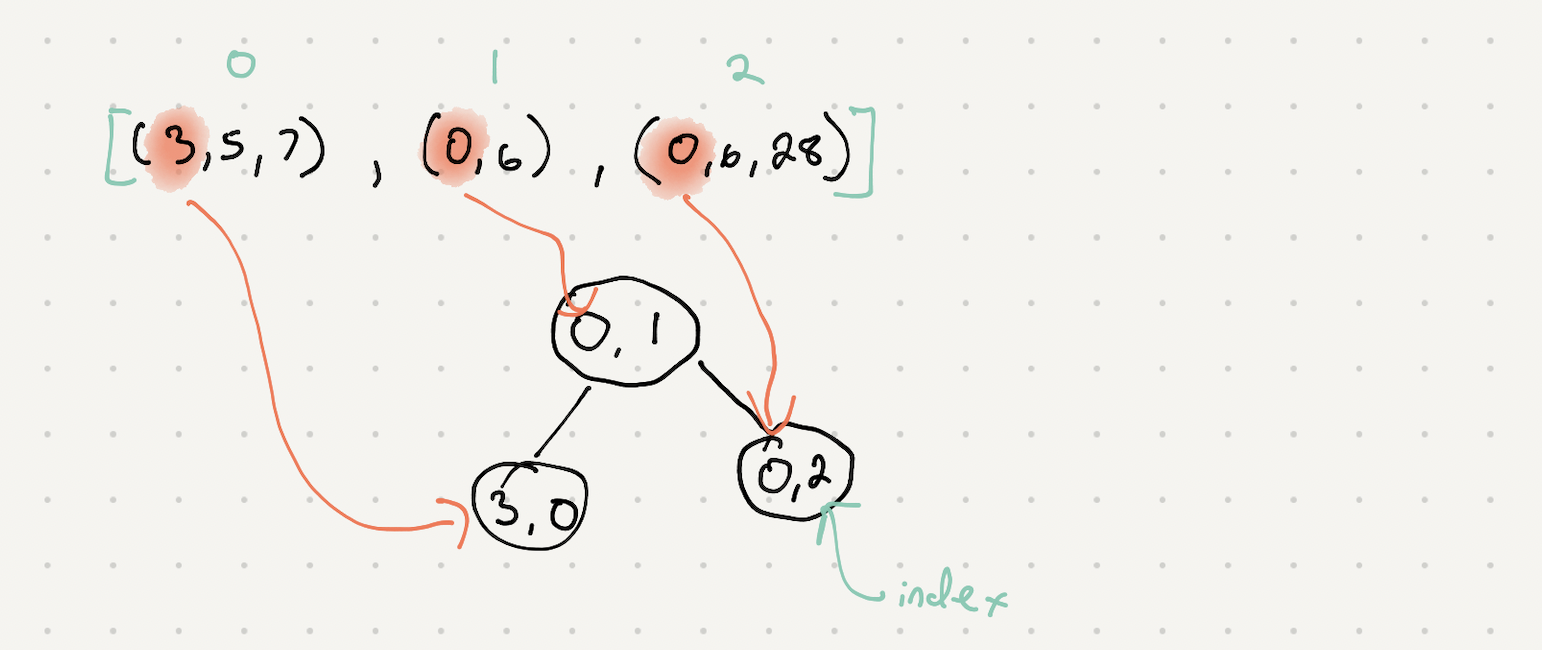
Now that we have some initial values we can also make the assumption that the min from this heap is the smallest possible number since all the sub lists are sorted. We can keep adding to our heap and keep popping until we have exhausted all numbers.

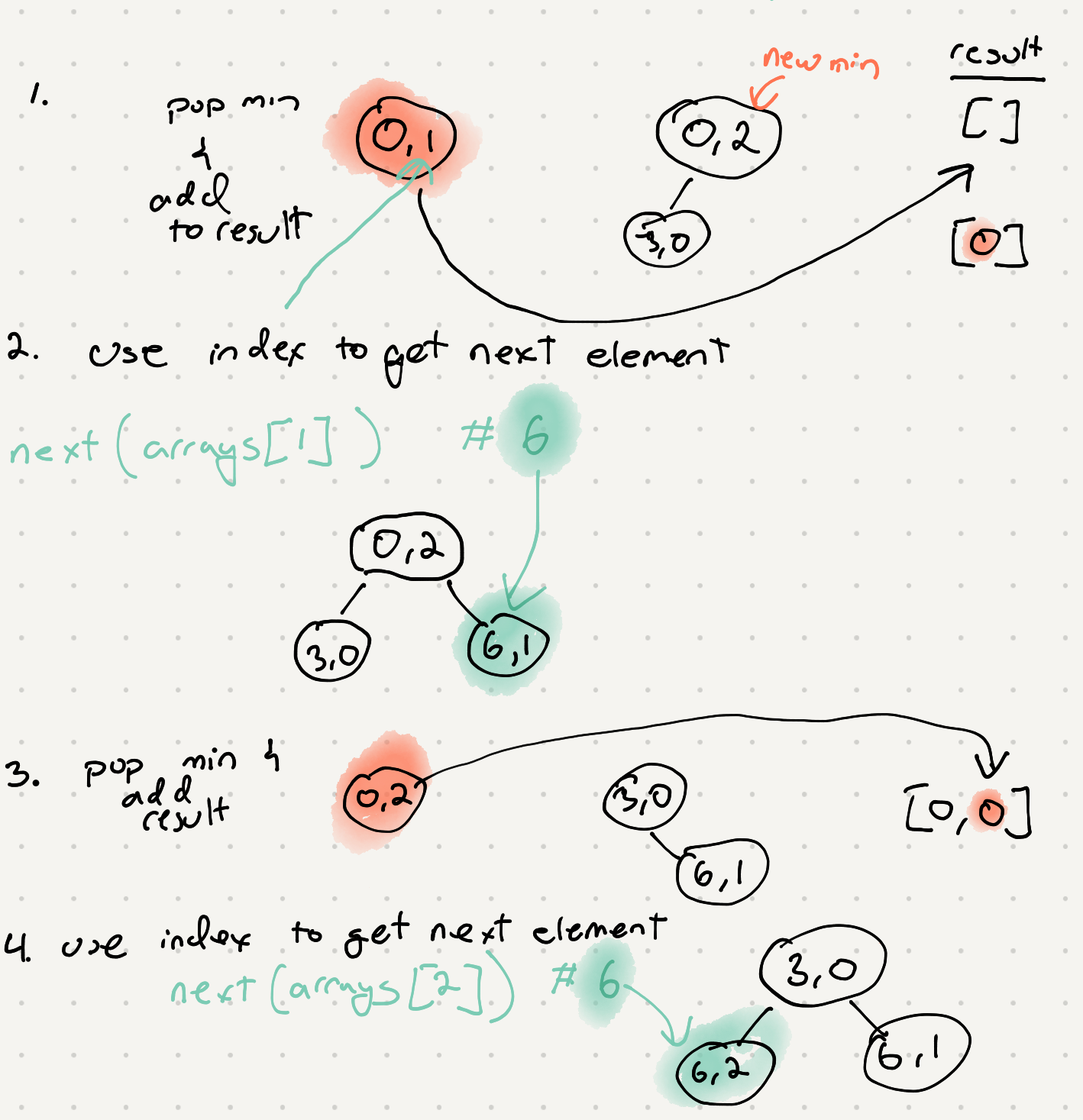
So we keep removing and adding things to the heap until we have exhausted all the elements from the sequences.

One cool python tool is the use of iterators. We can use them to manage combining lists of different sizes and not have to add guards for index errors.

i1 = iter([1,2,4])
i2 = iter([3,47])
i3 = iter([])

for it in [i1, i2, i3]:
    element = next(it, None)
    if element:
        print(element)


# 1, 3

So putting it all together the code will look like this:

import heapq

def merged_sorted_arrays(sorted_arrays)
    heap = []
    array_iterators = [iter(x) for x in sorted_arrays)]

    for index, it in enumerate(array_iterators):
        element = next(it, None)
        if element:
            heapq.heappush(heap, (element, i))

    result = []
    while heap:
        smallest_item_in_heap, array_index = heapq.heappop(heap)
        result.append(smallest_item_in_heap)

        next_item_to_add_to_heap = next(array_iterators[array_index], None)

        if next_item_to_add_to_heap:
            heapq.heappush(heap, (next_item_to_add_to_heap, array_index)]

    return result