Count all paths to a point in a grid

Problem statement

Given a 2d matrix and a starting position of (0,0) count all the possible paths to the target

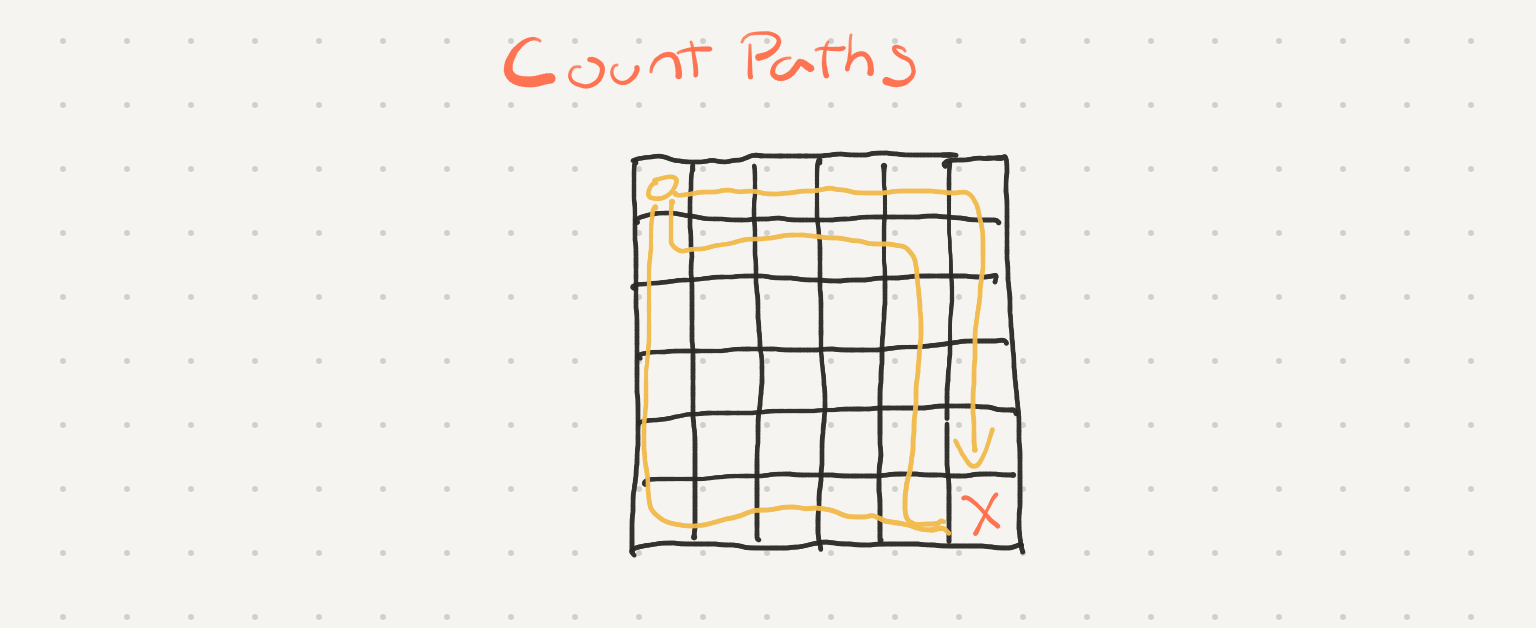
When we look at the way we would traverse through the grid we can only move to the right or downwards. Similar to the generate subsets problem we make a choice on right or down and enumerate all the paths.

If we were to put our starting position further in the grid we see the count is a sum of all the counts to the right and all the sums below.

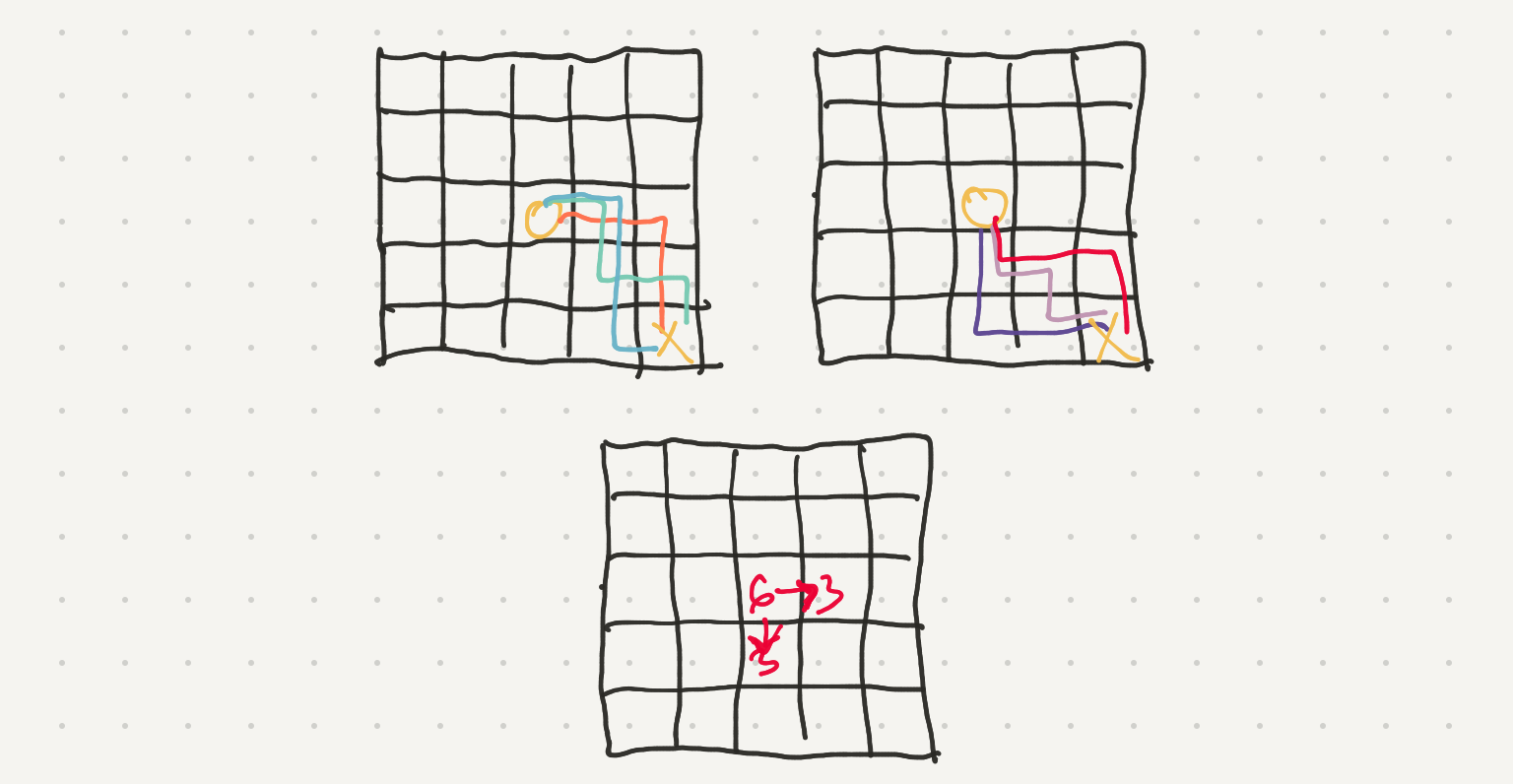
So we can solve this problem by moving forward in a direction and recursively getting all the counts and returning the summation. Here’s how the recursion tree would look like for this -

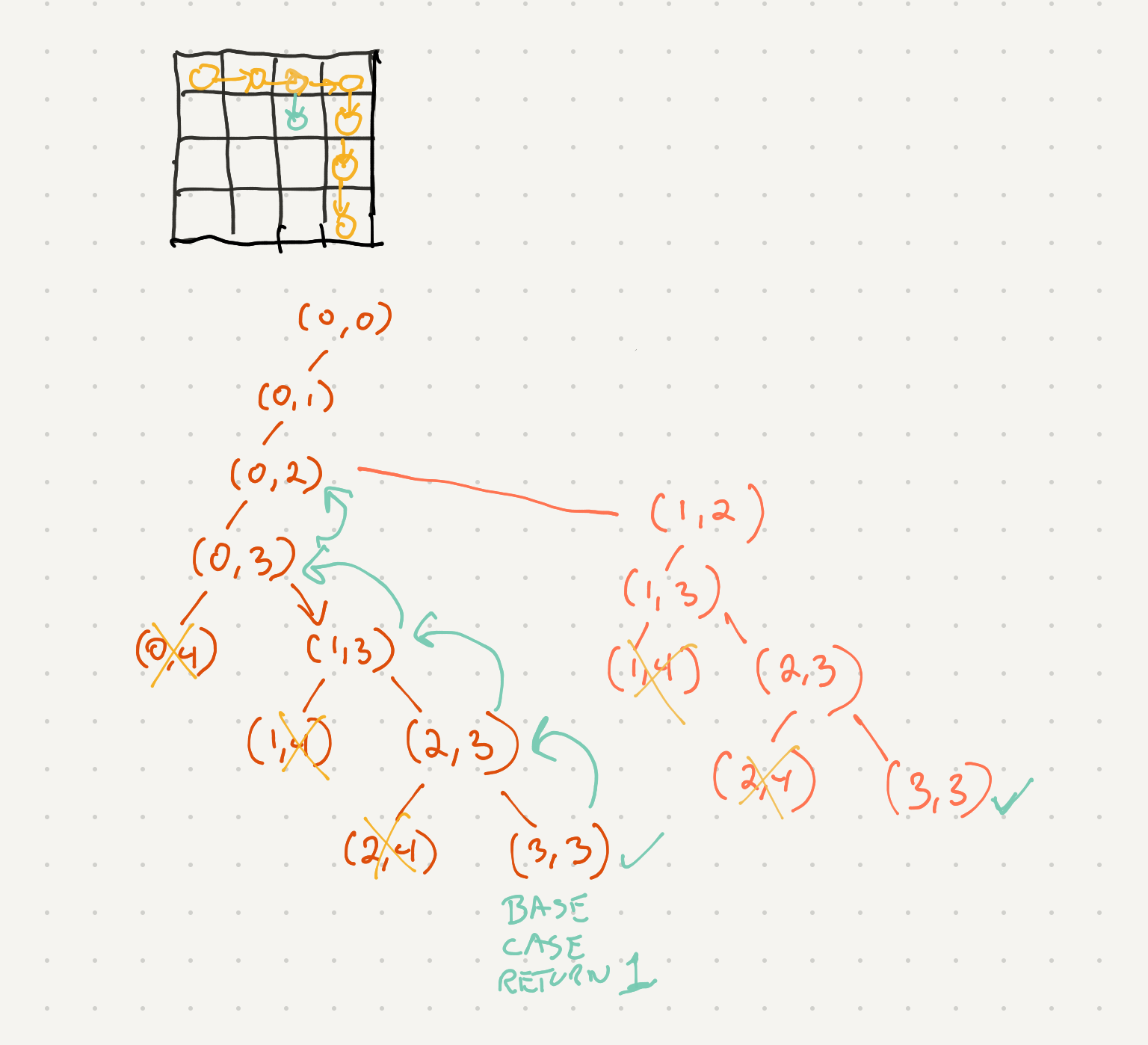
So we need a way to stop from going over the board. We can do this by figuring out the number of columns and rows and setting up some guards

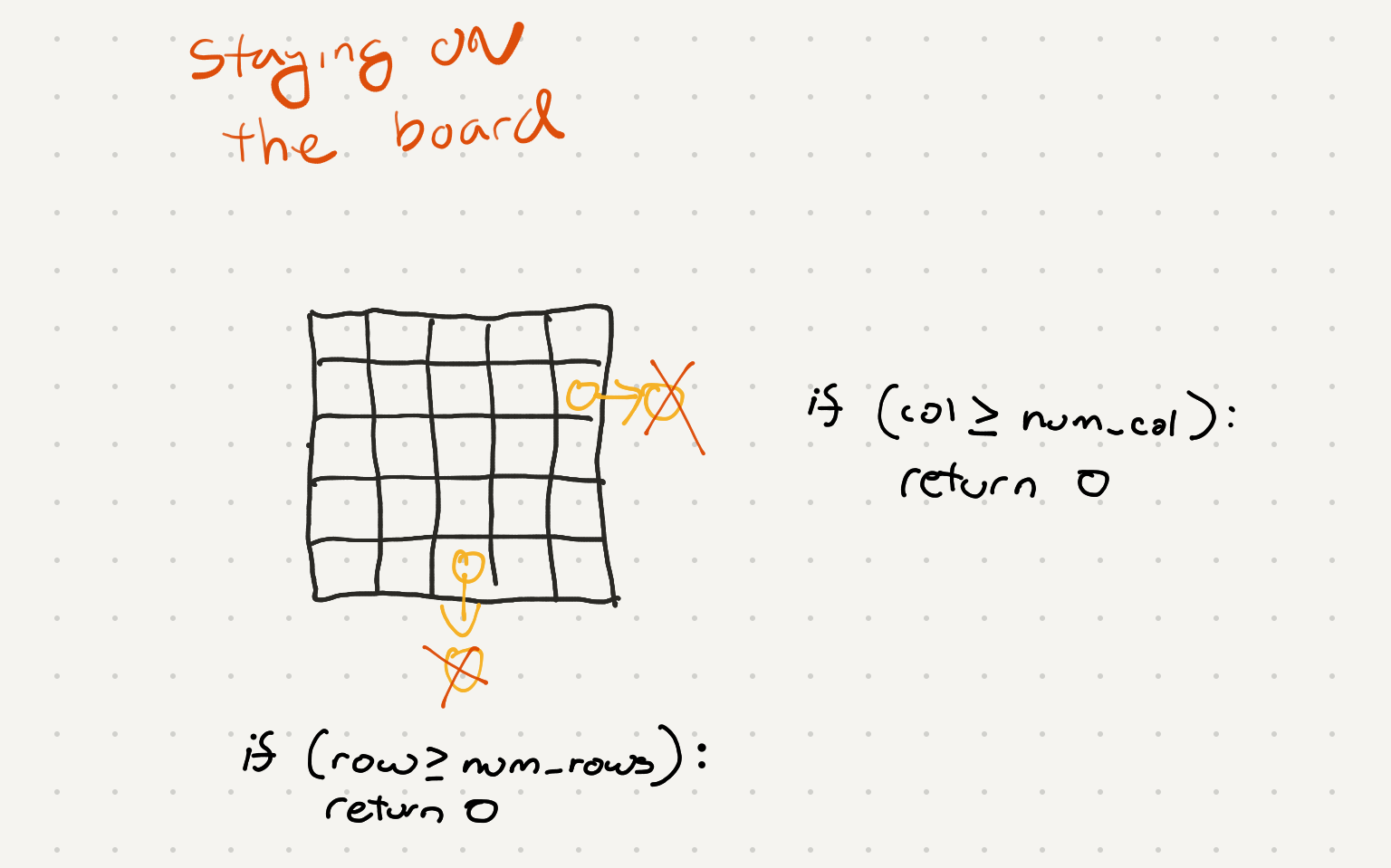
def count_paths(grid, row, col):
    num_col = len(grid[0])
    num_row = len(grid)

    # guards to prevent going over the grid
    if (row >= num_row) or (col >= num_col):
        return 0
	
    # found our target
    if (row == num_row) and (col == num_col):
    	return 1

    right_count = count_paths(grid, row, col+1)
    left_count = count_paths(grid, row+1, col)

    return right_count + left_count

Finally lets look at the time and space complexity