BST to doubly linked list

Problem statement

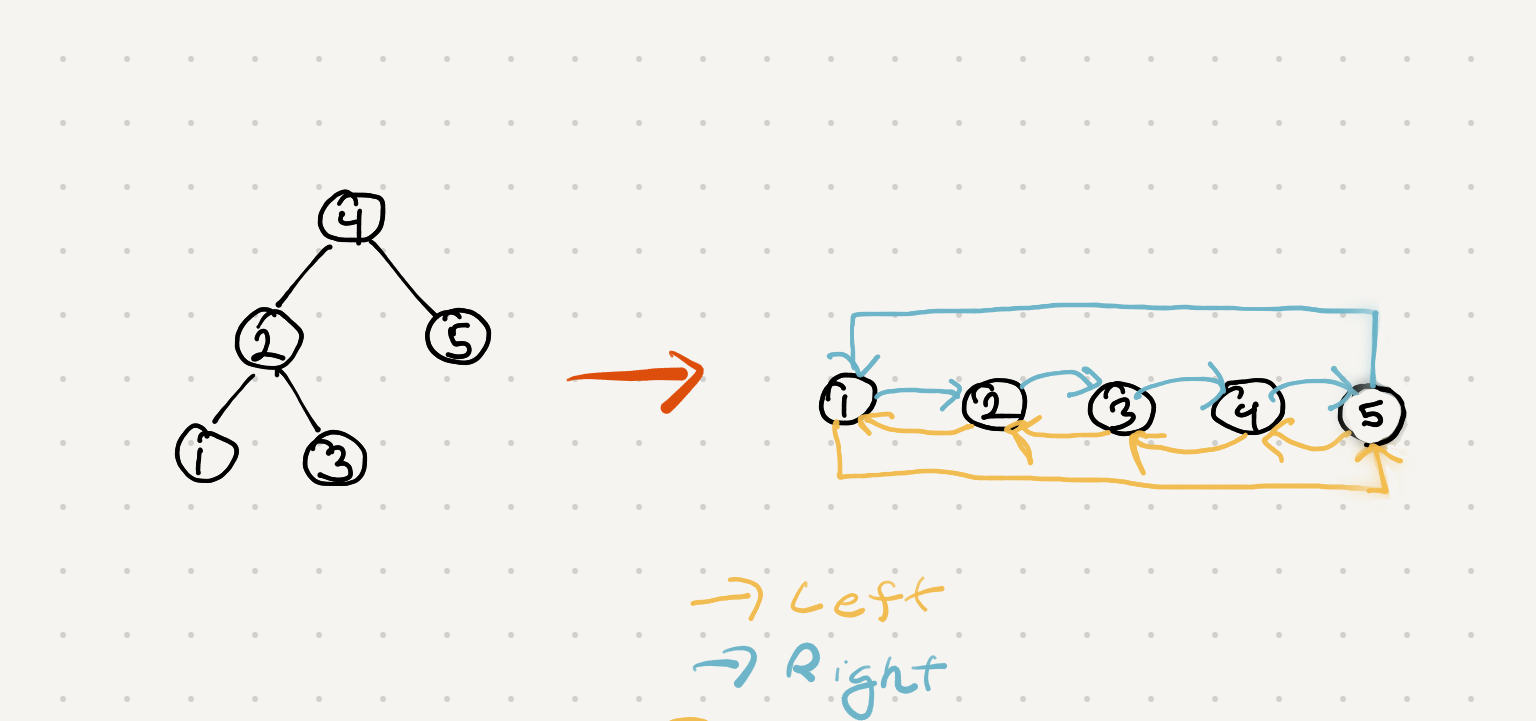
Write a function BTtoLL(TreeNode root) that takes a binary tree and rearranges its left_ptr and right_ptr pointers to make a circular doubly linked list out of the tree nodes in the in-order traversal order. The head of the list must be the leftmost node of the tree (since it is the first one in the in-order traversal) and the tail of the list must be the rightmost node of the tree. Tail’s “next” pointer must point to the head and head’s “previous” pointer must point to the tail (as circular doubly-linked lists go).

In the resultant data structure we will think of right_ptr as “next” pointer of the list and of left_ptr as the “previous” pointer of the list. Note that although the resultant data structure will consist of a bunch of TreeNode instances, it will not be a tree (because, as a graph, it will have cycles).

The function must not allocate any new TreeNode instances, it must not change existing TreeNodes’ values either. It must change left_ptr and right_ptr pointers of the existing TreeNodes to form the desired data structure.

So lets break down this example and see how to convert a much smaller tree/node.

For a single node the left and right pointers should point to itself What would converting a single node look like?

how about a two node?

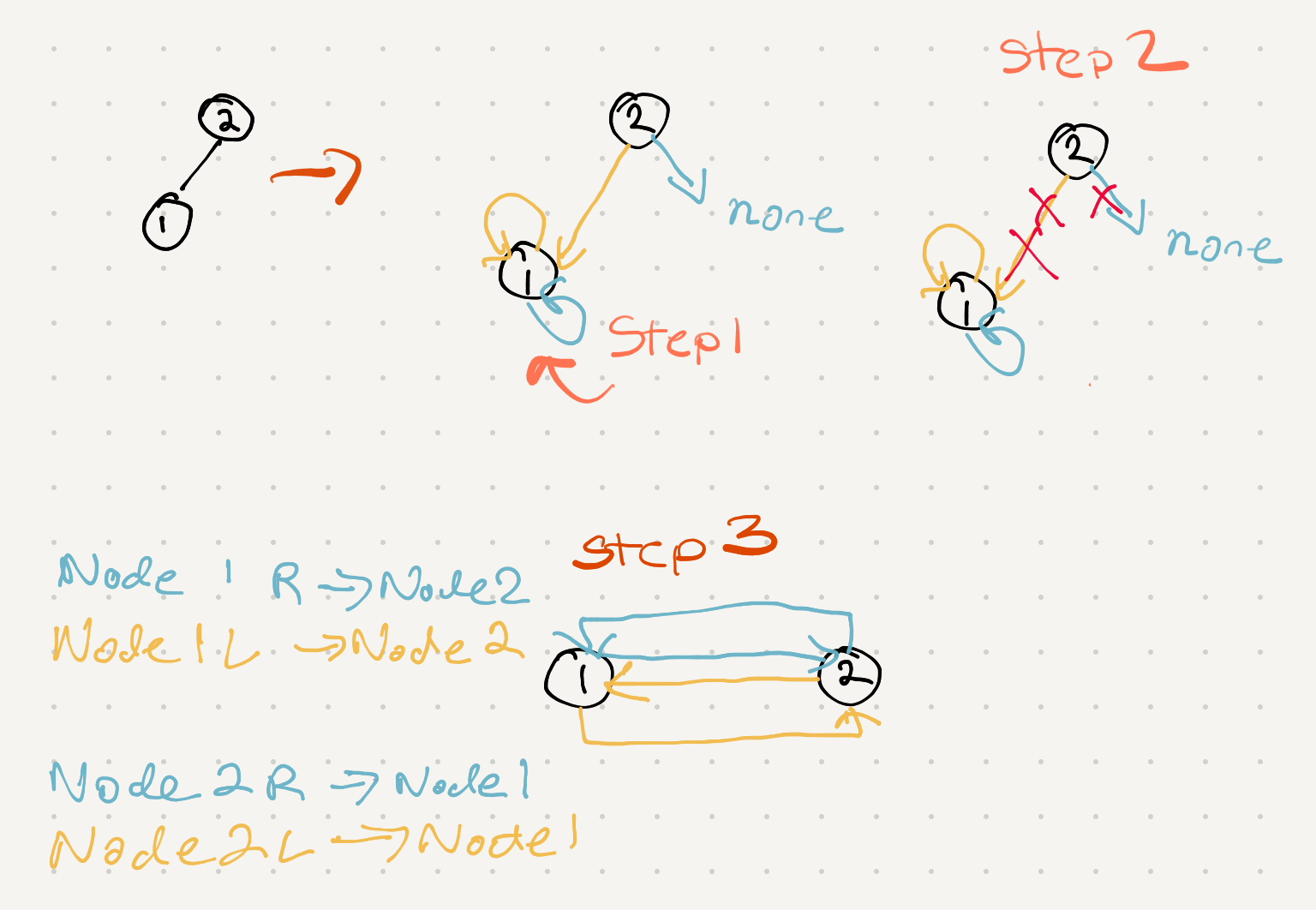
we need to be able to merge two nodes together and re-point nodes 1 left pointer to node 2, nodes 2 right pointer to node 1 to create the circular link

we can create a helper function that will merge two nodes

def mergeDLL(dll_1, dll_2):
    if not dll_1:
        return dll_2
    
    if not dll_2:
        return dll_1
        
    # connect end of dll_1 to head of dll_2
    dll_1_tail = dll_1.left_ptr
    dll_1_tail.right_ptr  = dll_2
    
    # update head and tail of the now connected LL
    dll_2_tail = dll_2.left_ptr
    
    dll_1.left_ptr = dll_2_tail
    dll_2_tail.right_ptr = dll_1
    
    return dll_1

how about a three node?

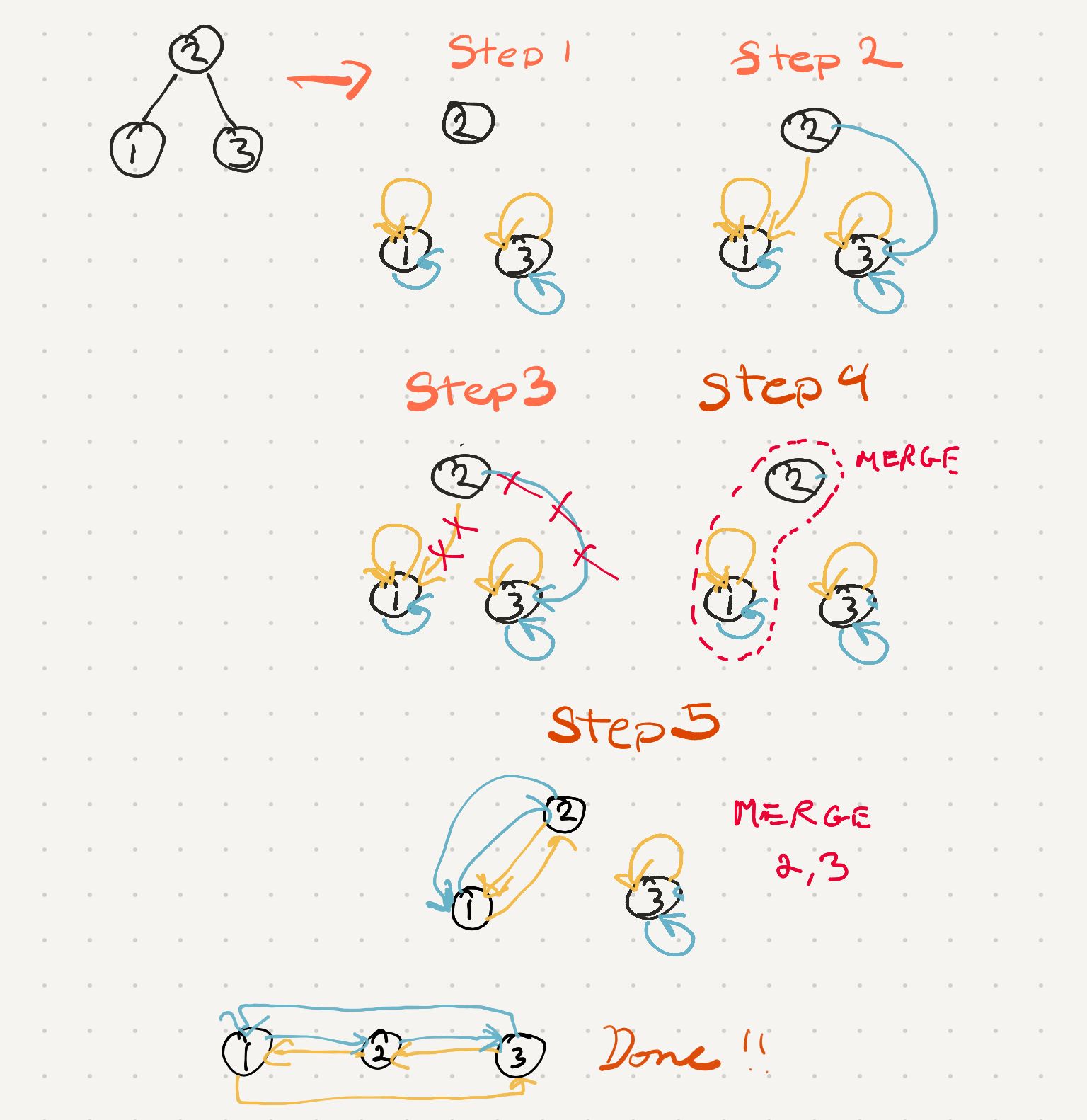
Now that we have our helper function we could solve this for 3 nodes and then n number of nodes

def BTtoLL(root):
    # base case
    if not root:
        return None
	
    # lets recursively call our function to get us a circular DLL for both left and right nodes
    L_head = BTtoLL(root.left_ptr)
    R_head = BTtoLL(root.right_ptr)
    
    # disconnect root
    root.left_ptr = root
    root.right_ptr = root
    
    # lets merge the left node and root and finally merge 3 dlls
    tmp_dll = mergeDLL(L_head, root)
    final_dll = mergeDLL(tmp_dll, R_head)
    
    return final_dll

Since we’re doing a traversal of the entire tree our time complexity will be O(n) and our space complexity will also be O(n) because memory used in recursion stack