Heapsort - step by step

Before we can step through heapsort we need to understand binary heaps / priority queues and their properties.

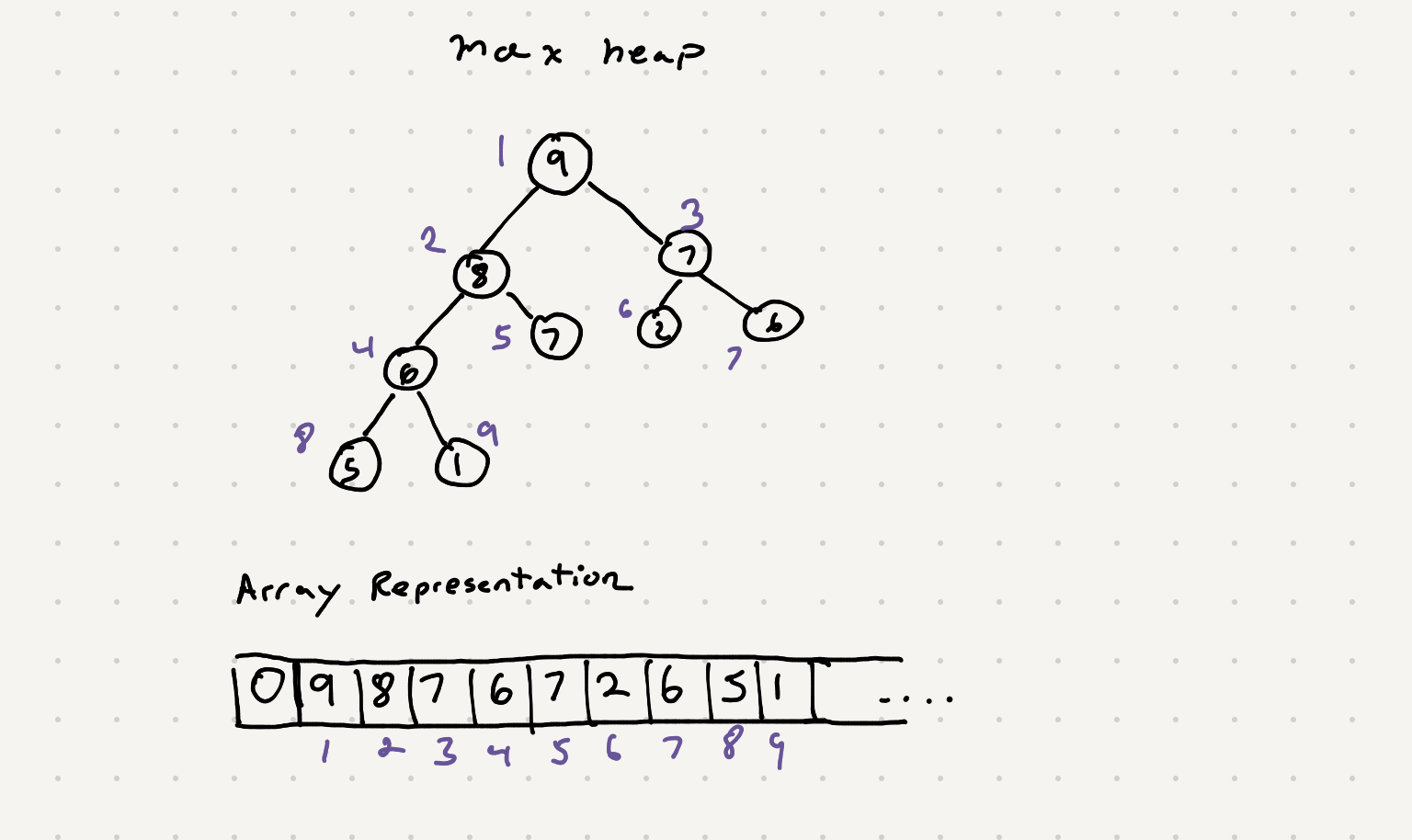
Heap properties

• Parent node is always >= it’s two leaf nodes
• Heaps are left almost complete trees

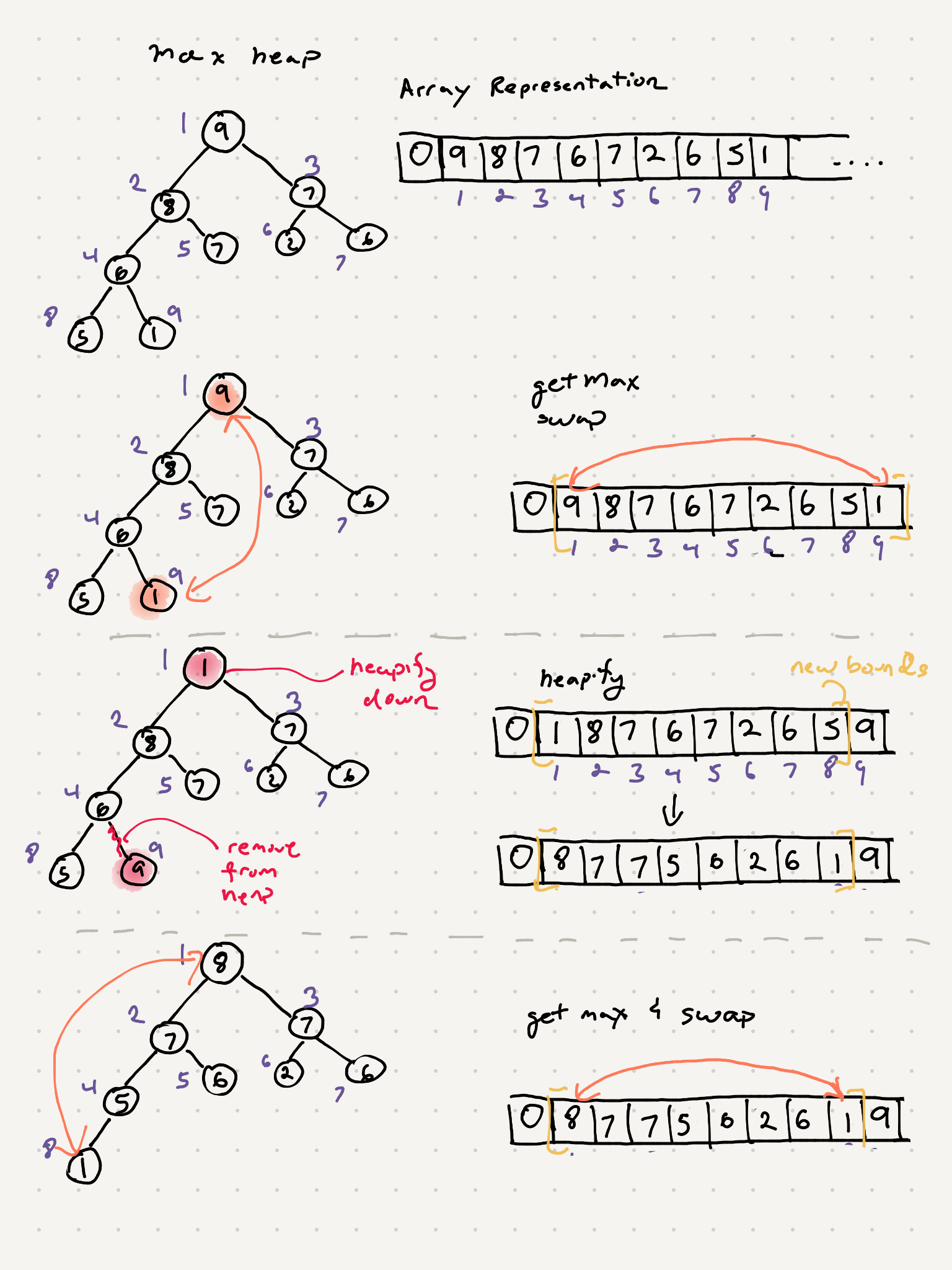
Even thought this heap is a tree it can be represented via an array. We can quickly access parents and leaves by doing some arithmetic.

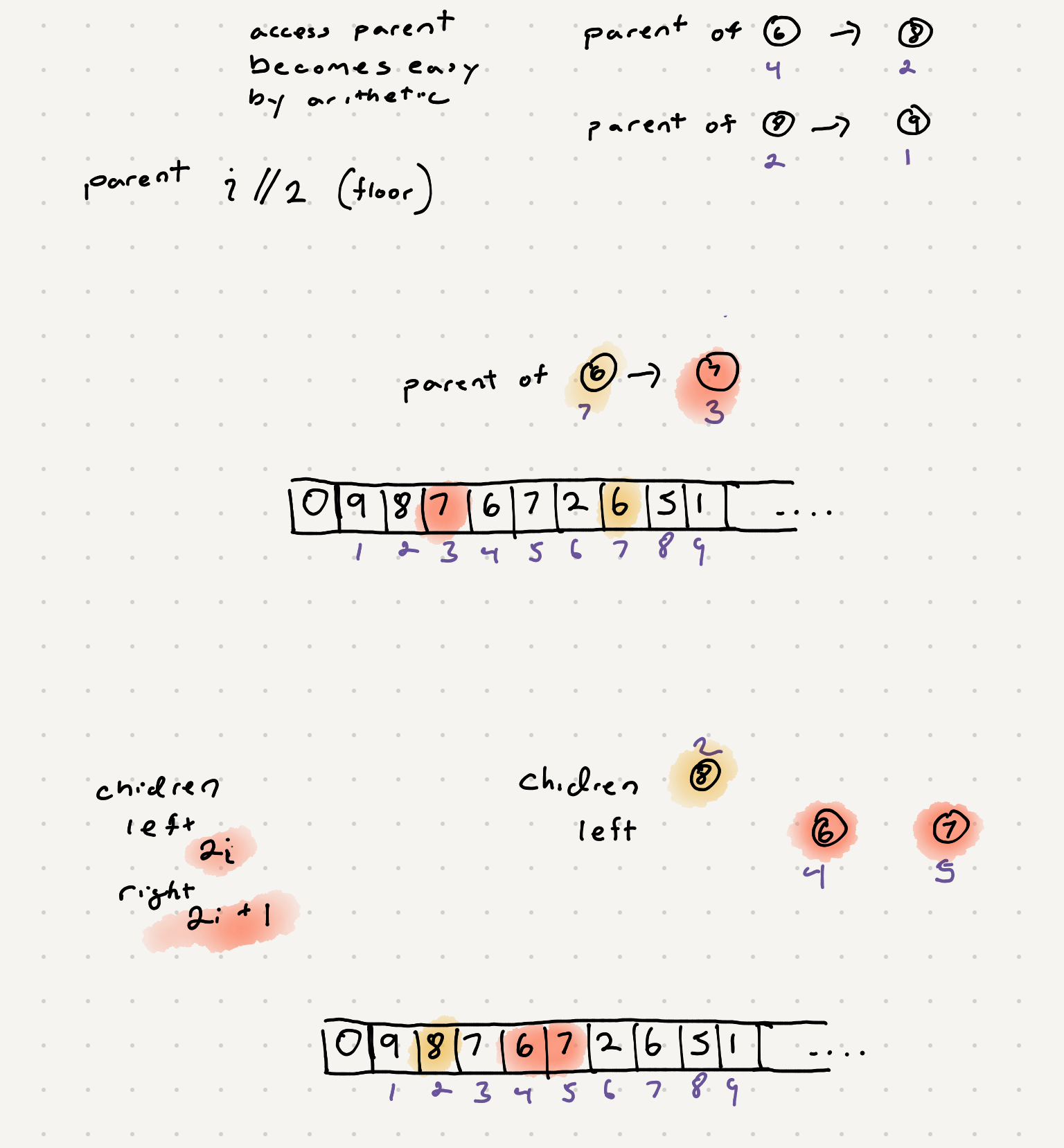
So we now can access parent and child nodes pretty easily. Let’s try adding some elements to our max heap

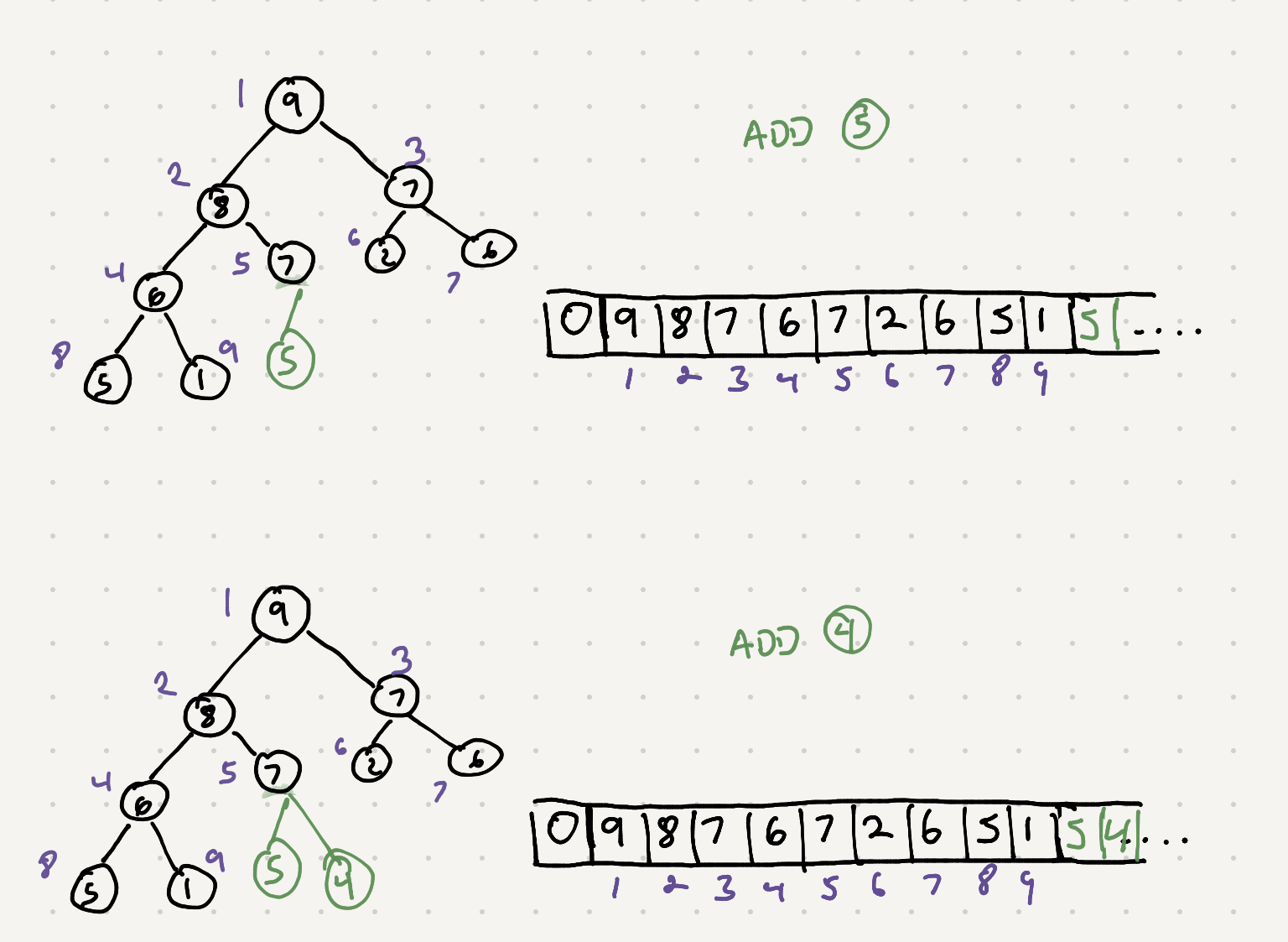
So far we’ve added nodes that maintain the properties of the max heap ie the values we added are smaller than their parent nodes. What about if we add a vvalue that needs to be higher in the tree?

When we add an element to the max heap we need to do an operation called heapify_up(also known as bubble-up, percolate-up, sift-up, trickle-up, swim-up, heapify-up, or cascade-up).

source for this algo - wiki for binary heaps:

1. Add the element to the bottom level of the heap at the most left.
2. Compare the added element with its parent; if they are in the correct order, stop.
3. If not, swap the element with its parent and return to the previous step.

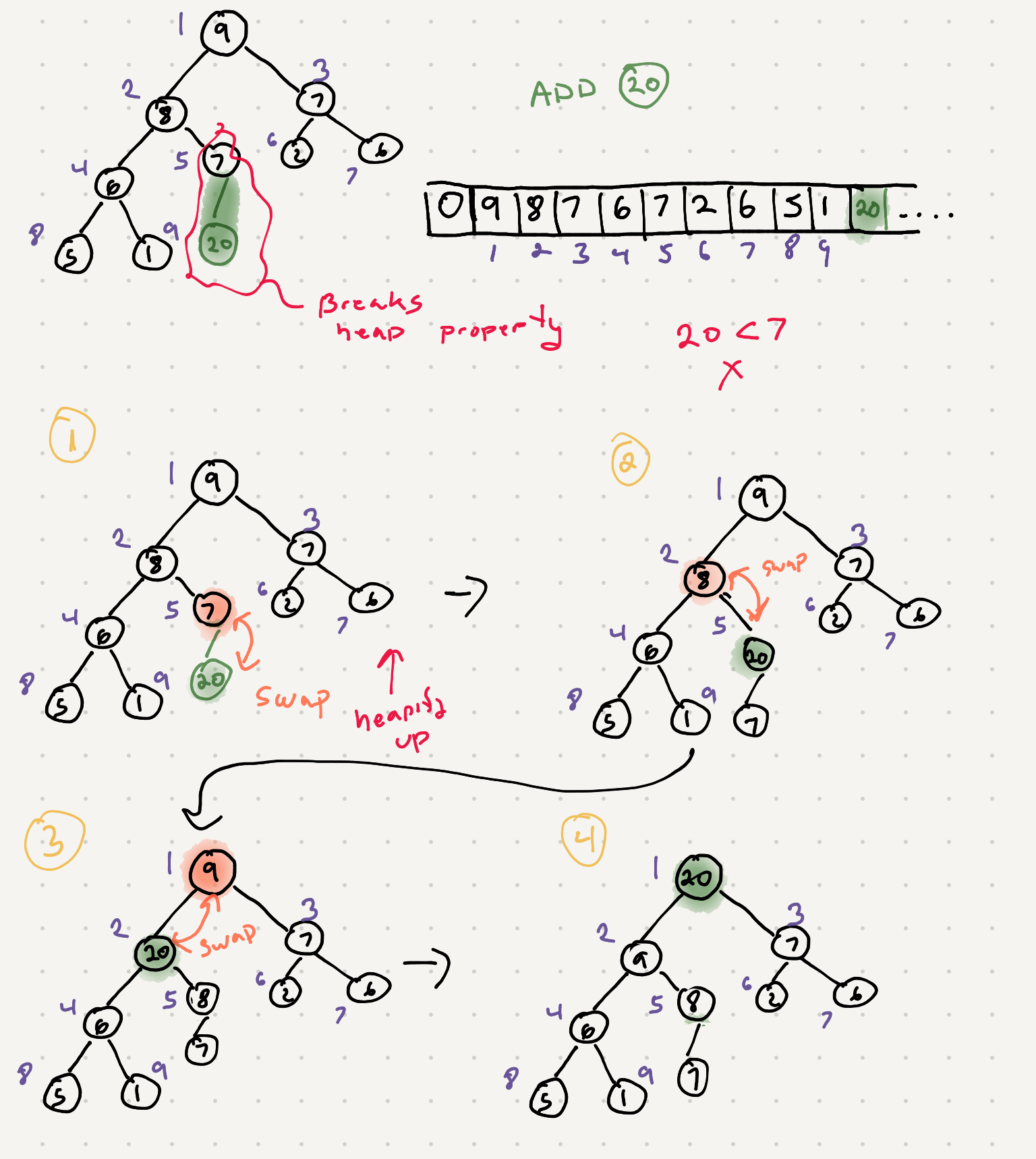
The insert has a worst-case time complexity of O(logn)

Now what about if we wanted to extract out the highest values from our max heap? We can do the corresponding heapify_down algorithm

1. Replace the root of the heap with the last element on the last level.
2. Compare the new root with its children; if they are in the correct order, stop.
3. If not, swap the element with one of its children and return to the previous step. (Swap with its smaller child in a min-heap and its larger child in a max-heap.)

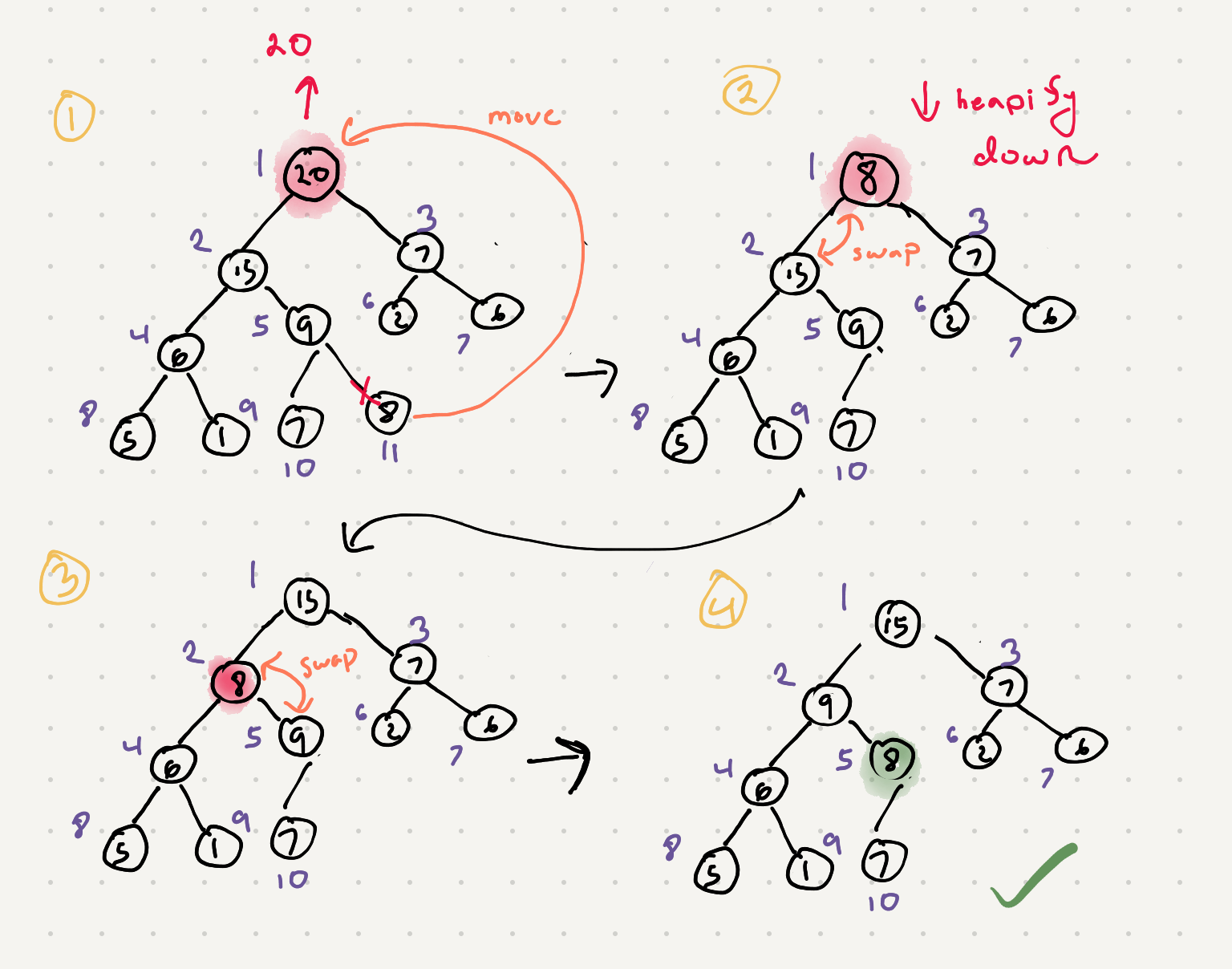
Ok so we now understand heaps a bit more. How do we use it to actually sort an array?

It boils down to a few major steps.

1. Build a heap from the array. This can be done in an O(n) operation. The normal heap insert is O(logn) but there is a way to do the build a bit faster.
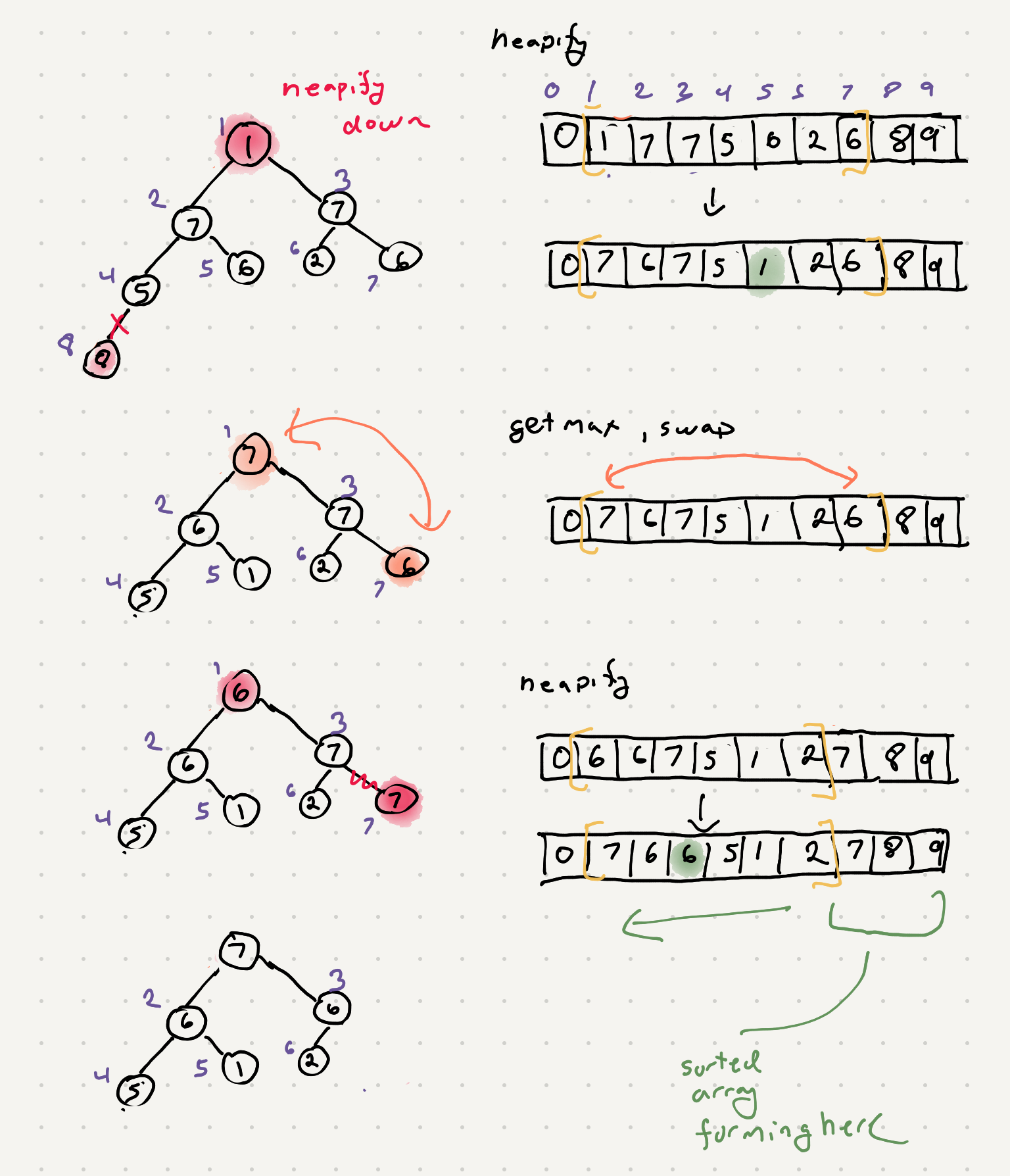
2. Swap the first item of the list with the last item. Decrease the range of our max heap
3. At this point our max heap is broken because of the swap. We need to heapify down to fix the max heap
4. Keep going back to step 2 until we finish processing the entire array

Let’s go through this visually

def heapify(arr, n, i):
    # Find largest among root and children
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2 
 
    if (l < n) and (arr[i] < arr[l]):
        largest = l
 
    if (r < n) and (arr[largest] < arr[r]):
        largest = r
 
    # If root is not largest, swap with largest and continue heapifying
    if largest != i:
        arr[i],arr[largest] = arr[largest],arr[i]
        heapify(arr, n, largest)
 
def heapSort(arr):
    arr_length = len(arr)
 
    # build max heap
    for i in range(arr_length, 0, -1):
        heapify(arr, arr_length, i)
 
    
    for i in range(arr_length - 1, 0, -1):
        # swap
        arr[i], arr[0] = arr[0], arr[i]  
        
        # heapify root element
        heapify(arr, i, 0)