Edit distance (Levenshtein) Pt 1

Problem Statement:

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2. You have the following 3 operations permitted on a word:

1. Insert a character
2. Delete a characterA
3. Replace a character

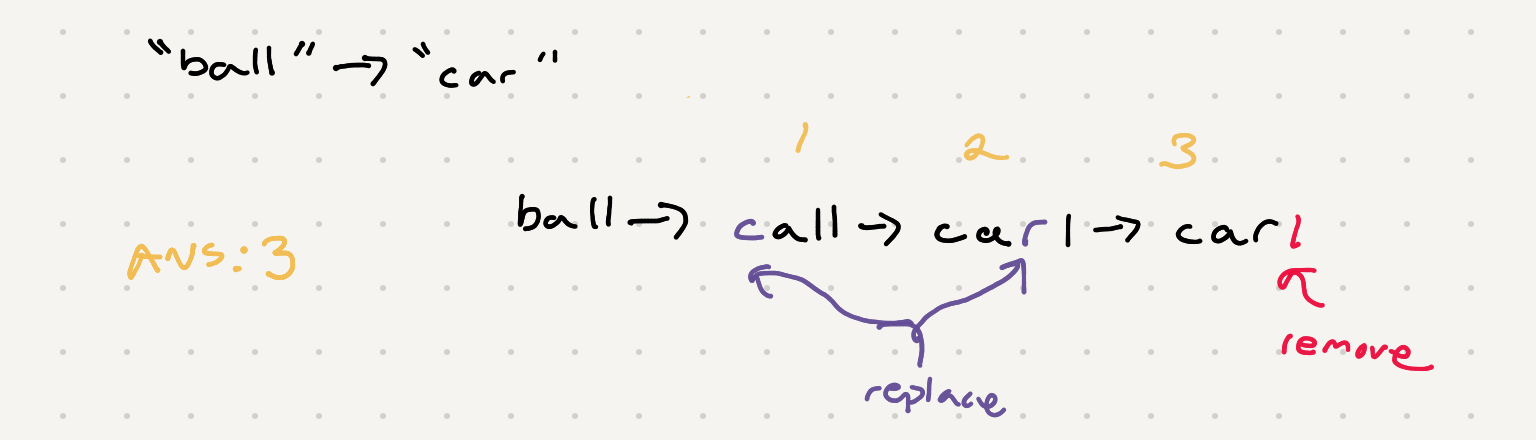
So at each letter we have to make a choice between our 3 edit options. We also have to think about the case where there is already a letter in both words. We’ll come back to the latter further down. My first thought was to use replace only to get us to the target word but there are moves we can do that would yield a smaller amount of moves such as -

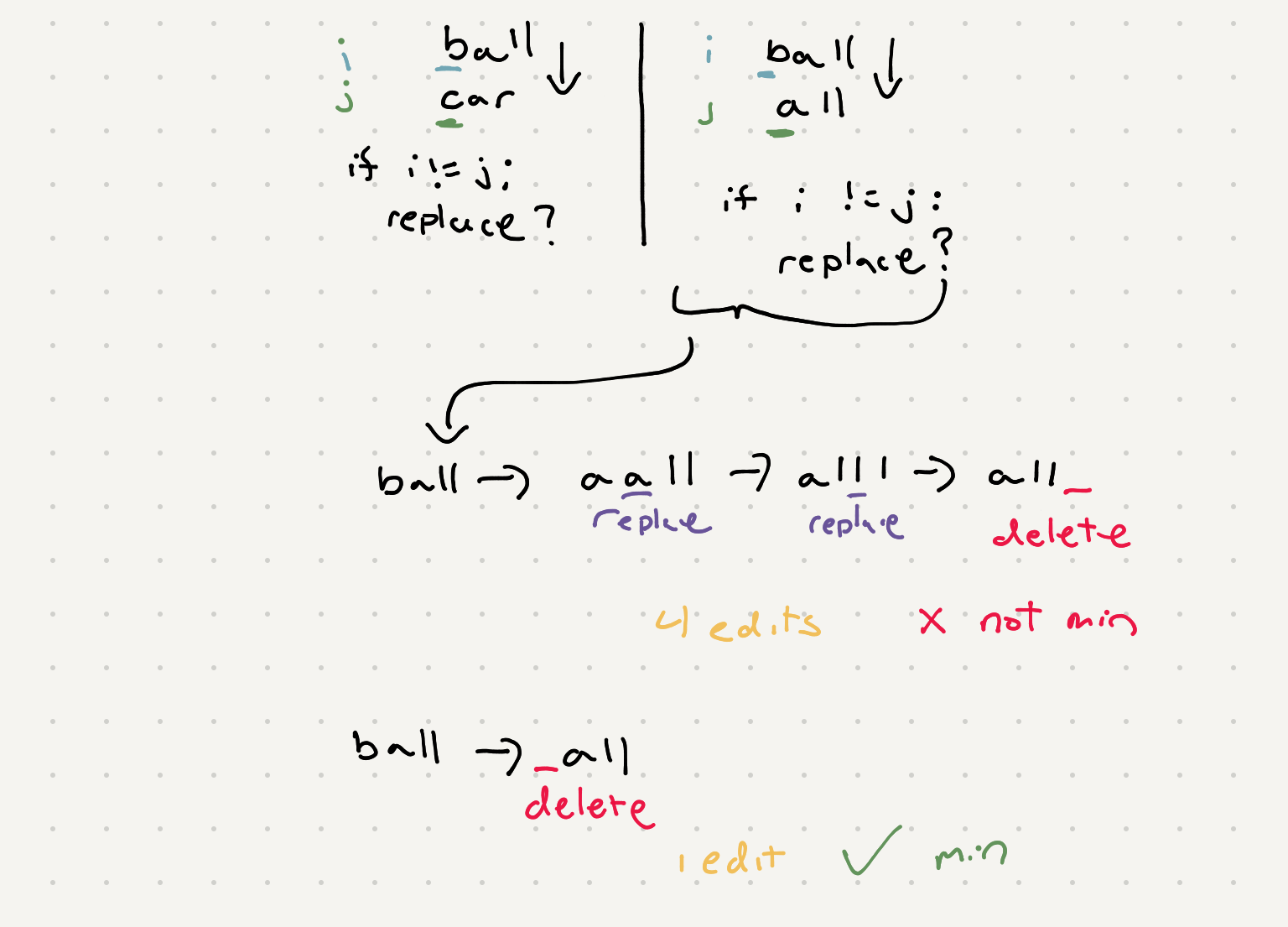
For now let’s try to formulate a recursive formulation that tries all these different options so we can get the minimum and also breaks the problem into sub-problems.

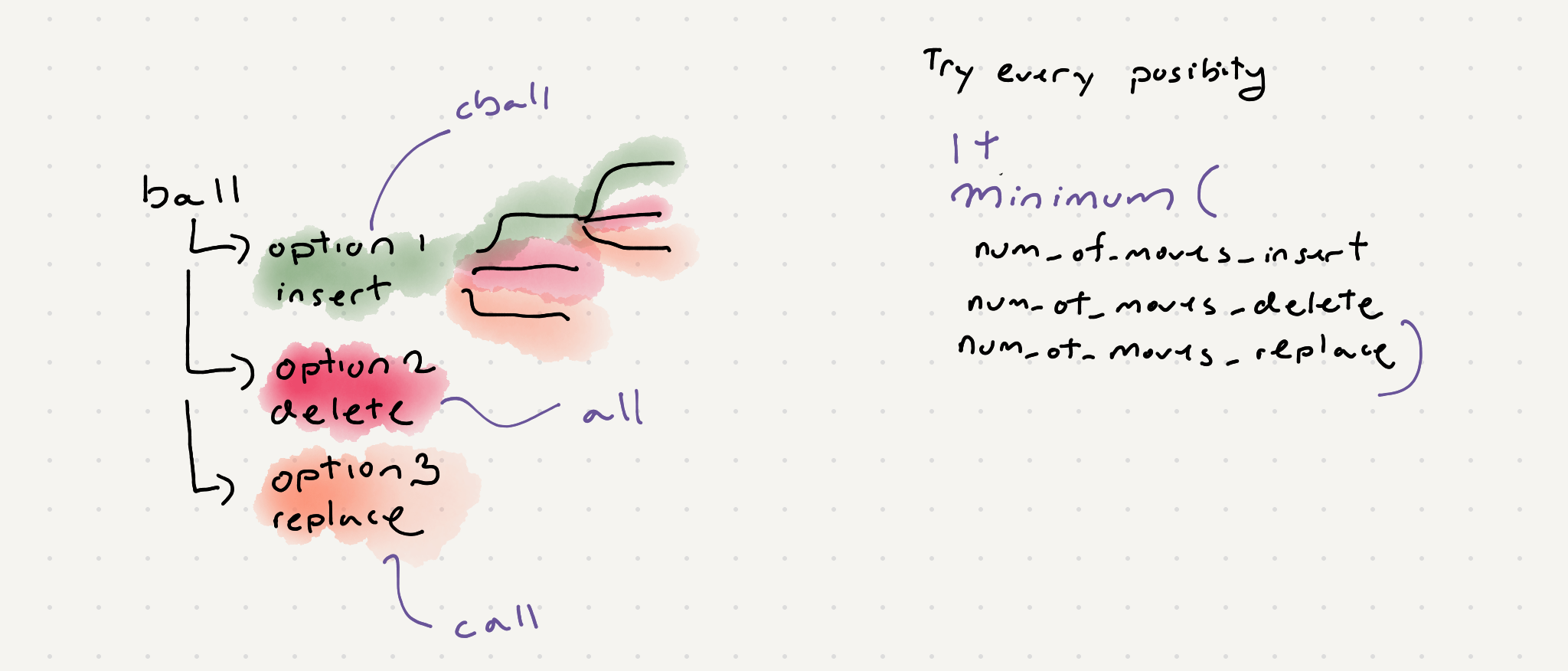
So let’s take a look closely at our different operations insert

ball -> cball
^
|
i = 0

We inserted the c so we only need to figure out how to make "ball" into "ar"
car        car 
^           ^
|           |
j = 0       j = 1

So we actually increased the size of our subproblem for word 1 but we did reduce our word2 which is the main conversion goal. So i doesn’t change

delete

ball -> all     ball
^                ^
|                |
i = 0            i = 1

car         
^           
|          
j = 0       

We deleted b so we only need to figure out how to make “all” into “car”. j doesn’t change because we still don’t have anything from “car” addressed

replace

ball -> call     call
^                ^
|                |
i = 0            i = 1

car              car
^                 ^
|                 |
j = 0             j = 1 

Letters are the same

We replace “b” with “c”. With this move we changed word1 and addressed a letter in word2. This means both i and j change

What happens however if both letters match? Well in this chase we shouldn’t count this as a move but should increment both i and j so we can look at the next set of records

So to summarize

1. insert f(i,j) -> f(i+1, j)
2. delete f(i,j) -> f(i+1, j)
3. replace f(i,j) -> f(i+1, j+1)
4. no edit needed f(i,j) -> f(i+1, j+1)

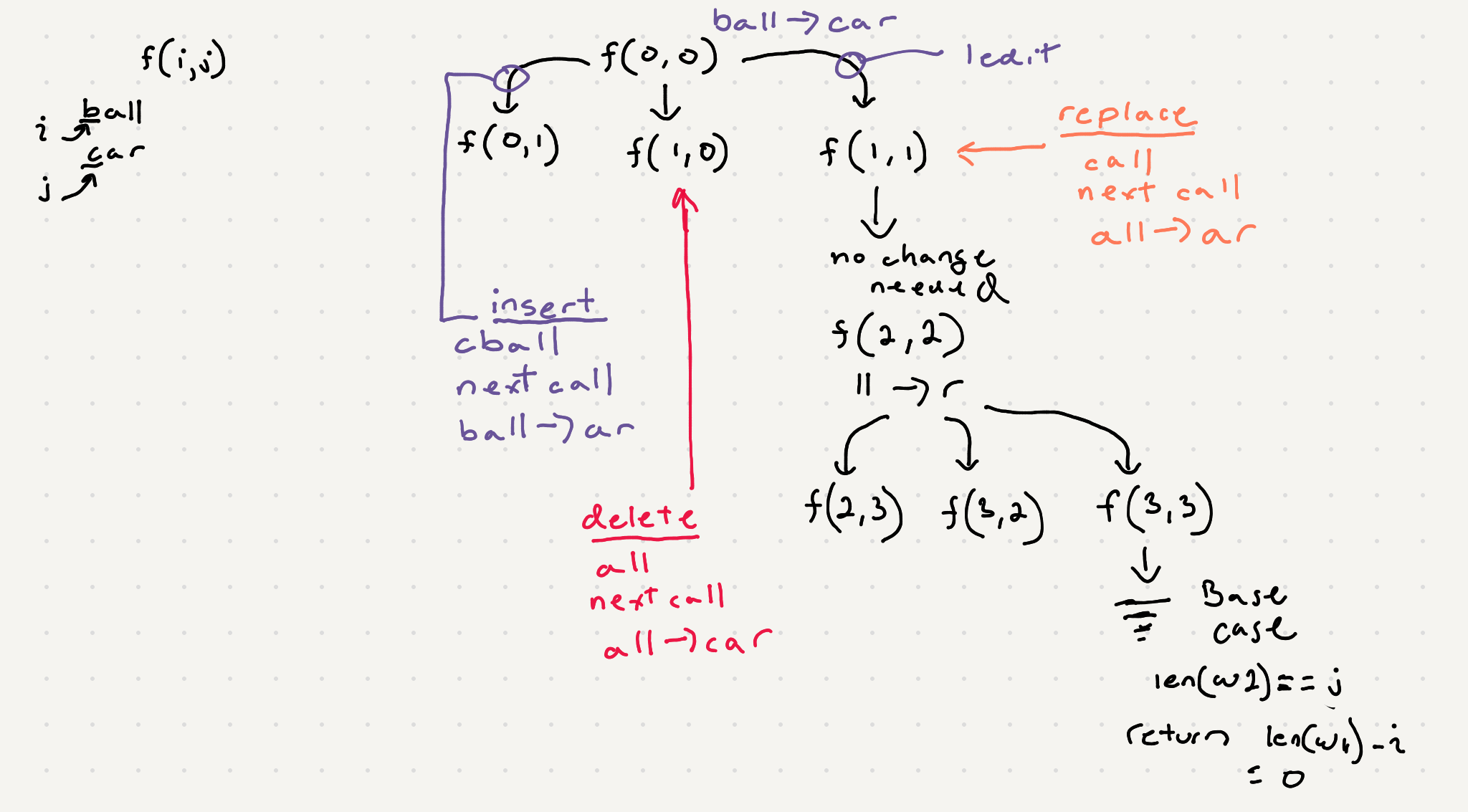
Lets also look at some base cases -

input is empty but word2 still has letters to process
ex. w1: “”, w2: “bat”
len(w2) - j

word2 is empty ie we need to delete all the characters in word1
ex. w1: bat, w2: ""
len(w1) - i

Putting it all together we have

def editDistance(word1: str, word2:str, i: int, j: int):
    if i == len(word1): 
        return len(word2) - j
    

    if j == len(word2): 
        return len(word1) - i 

    if word1[i] == word2[j]:
        return editDistance(word1, word2, i + 1, j + 1) 
        
    # +1 because the function will return the edit distance with the subset of letters
    # and we need to include the edit within this stack frame
    return 1 + min(editDistance(word1, word2, i, j + 1),           # Insert 
                    editDistance(word1, word2, i + 1, j),          # Replace 
                    editDistance(word1, word2, i + 1, j + 1))      # Delete

# driver
editDistance(word1, word2, 0, 0)

The time complexity for this solution is O(3^n). This exponential solution isn’t ideal but in part 2 we’ll try to optimize this solution