N queens on a chess board

Problem Statement:

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other. Given an integer n, return all distinct solutions to the n-queens puzzle. Each solution contains a distinct board configuration of the n-queens' placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space respectively.

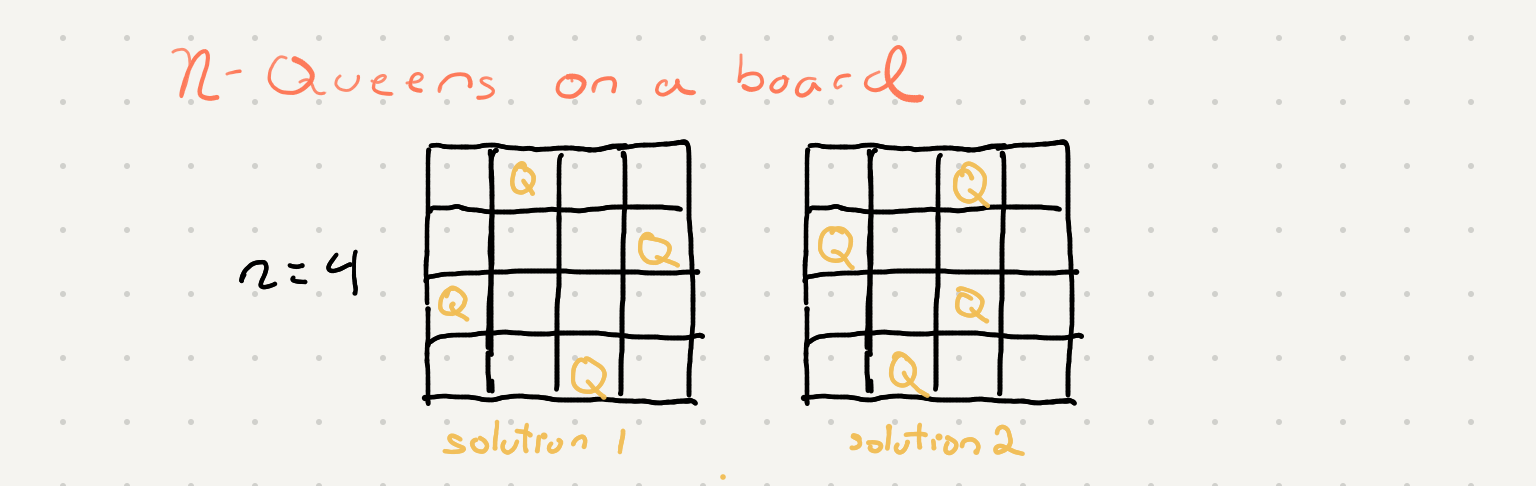
This was a difficult problem for me and took me some time to really understand. I had to make sure I fully understood recursion before fully understanding the solution.

First let’s make sure we understand how placing a queen changes the board. When you place a queen on the board the queen will block everything horizontally, vertically and diagonally like so -

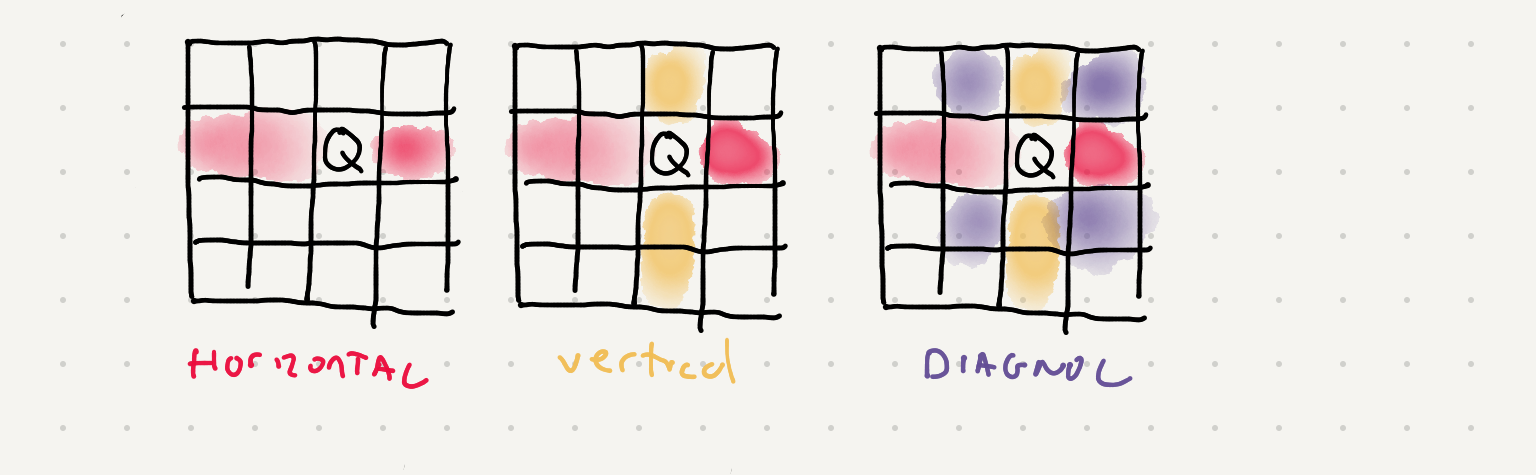
So after each placement the number of cells we have available to place other queens gets smaller and smaller. Let’s try to solve this by hand -

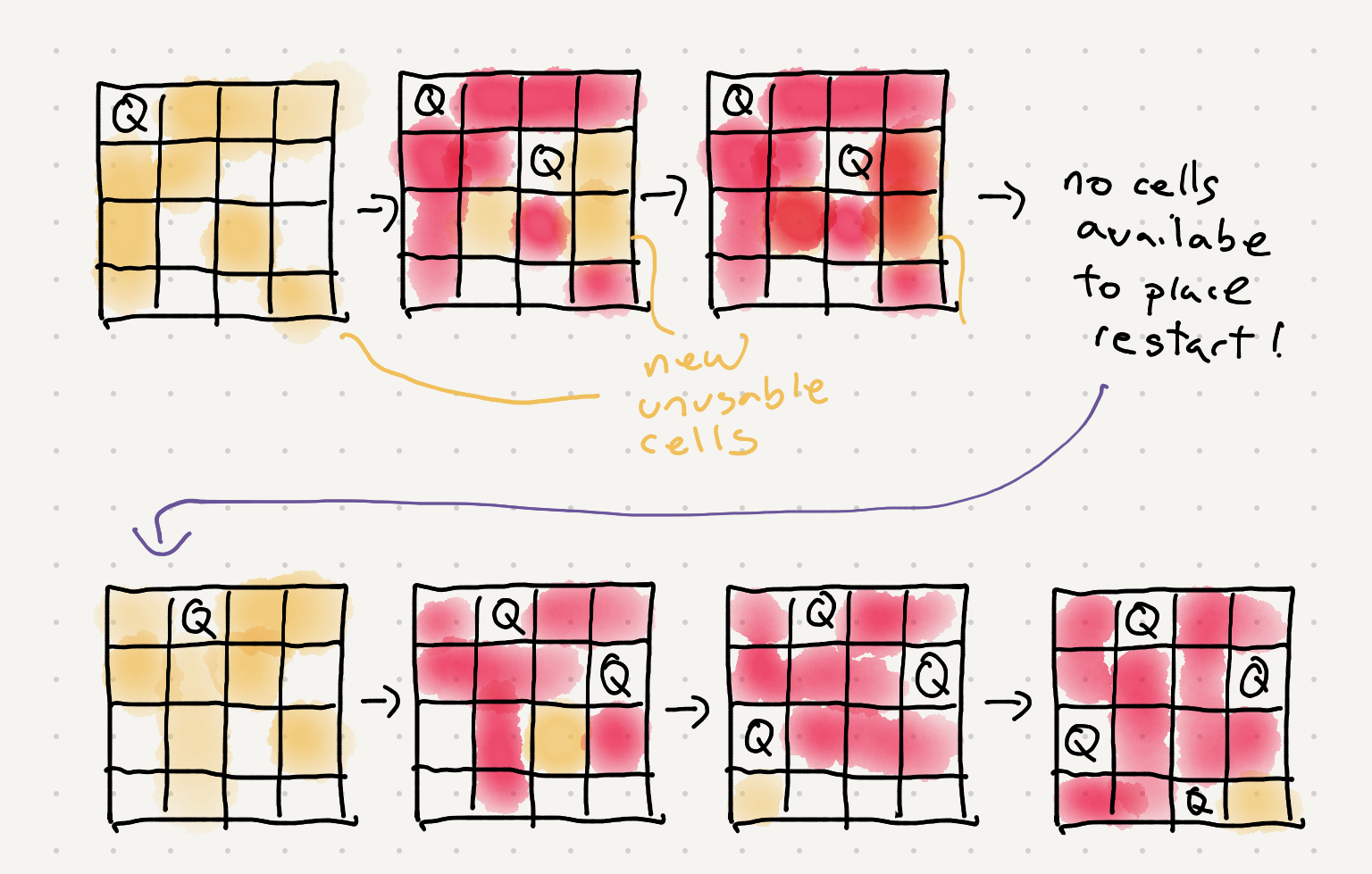
So what did we really do in our manual solution?

    1. We placed a queen
    2. We moved to the next row and only put a queen where the queen wouldn’t be in the line of sight of other queens
    3. We got to a point where our first idea didn’t work and restarted
    4. We removed the placement that failed and tried another available slot and kept going
    5. We placed our final queen when we finished processing all rows

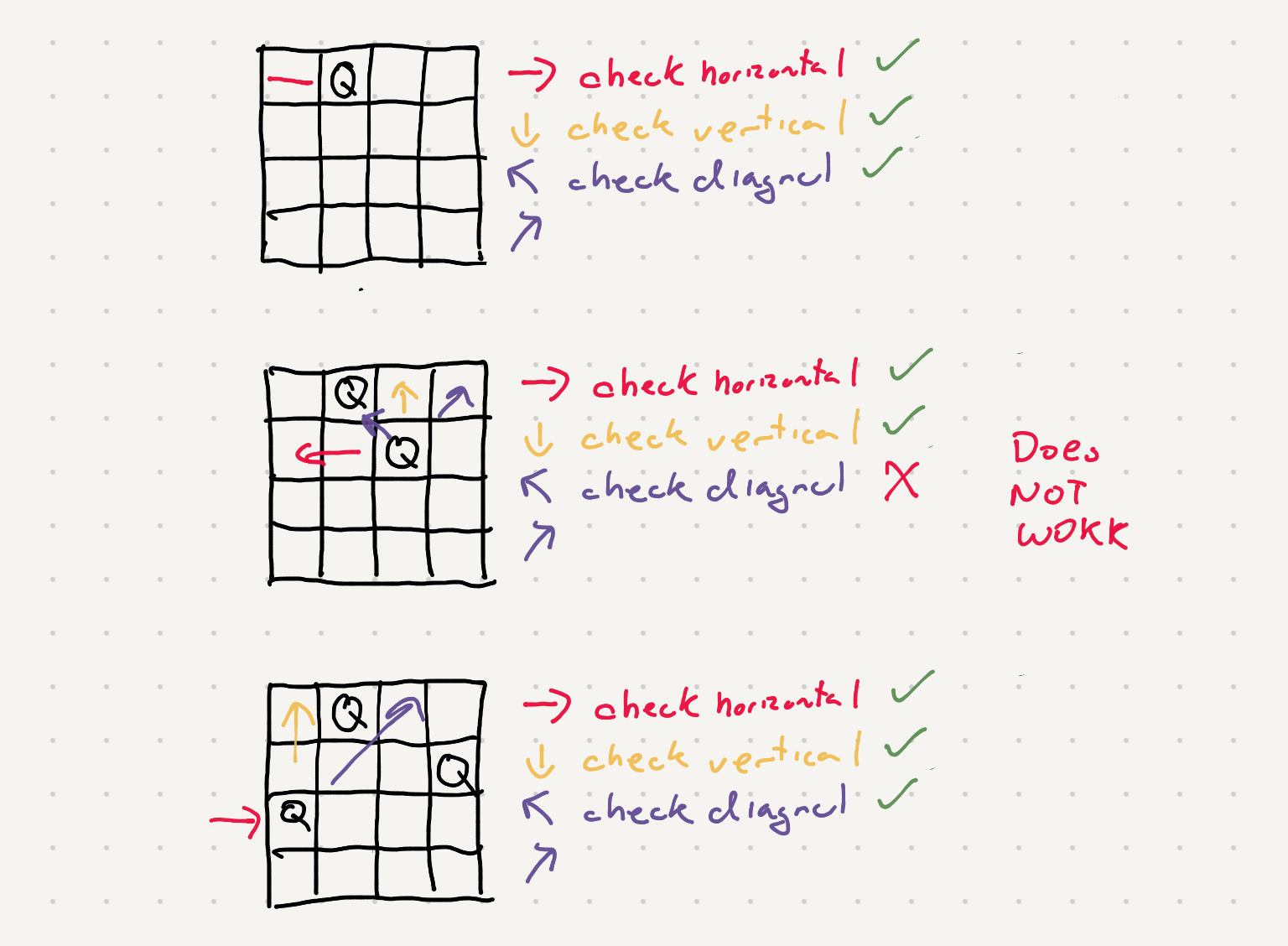
So this is backtracking problem. That means we have to go down a path and backtrack when we get to a place that isn’t going to give us our goal. In our manual solution we blocked of areas of the grid we aren’t allowed to place items anymore. In the code we instead looked at the board above the current (row, col) and check if there would be any queens collisions. The reason for this is to avoid maintaining state of the queens positions AND the grid locations that are not available to place a queen.

def solveNQueens(n: int) -> List[List[str]]:
    def valid_above(n, grid, row, col):
        # Check this row on left side 
        for i in range(col): 
            if grid[row][i] == 'Q': 
                return False

        # Check upper diagonal on left side 
        for i, j in zip(range(row, -1, -1), range(col, -1, -1)): 
            if grid[i][j] == 'Q': 
                return False

        # Check lower diagonal on left side 
        for i, j in zip(range(row, n, 1), range(col, -1, -1)): 
            if grid[i][j] == 'Q': 
                return False

        return True

    def n_queen(n, grid, row):
        if row == n:
            valid_grids.append([''.join(x) for x in grid])
            return

        # go through every row and place a queen
        for row in range(n):
            # check if the grid is valid only in the above direction
            if valid_above(n, grid, row, col):
                # place a queen
                grid[row][col] = 'Q'

                # recurse and increment to the next row
                n_queen(n, grid, col + 1)

                # remove the queen so we can try placing it in the next col
                grid[row][col] = '.'


    grid = [['.' for x in range(n)] for y in range(n)]
    valid_grids = []
    n_queen(n, grid, 0)

    return valid_grids