Generate course schedule w/ dependencies

Problem Statement:

You need to take n courses and a few of these courses have prerequisites. You are given the prerequisites as a list of pairs where each pair represents the course and the dependent course you need to have taken to take that course. Give N and the pre requisites generate a schedule. If no schedule can be generated return -1

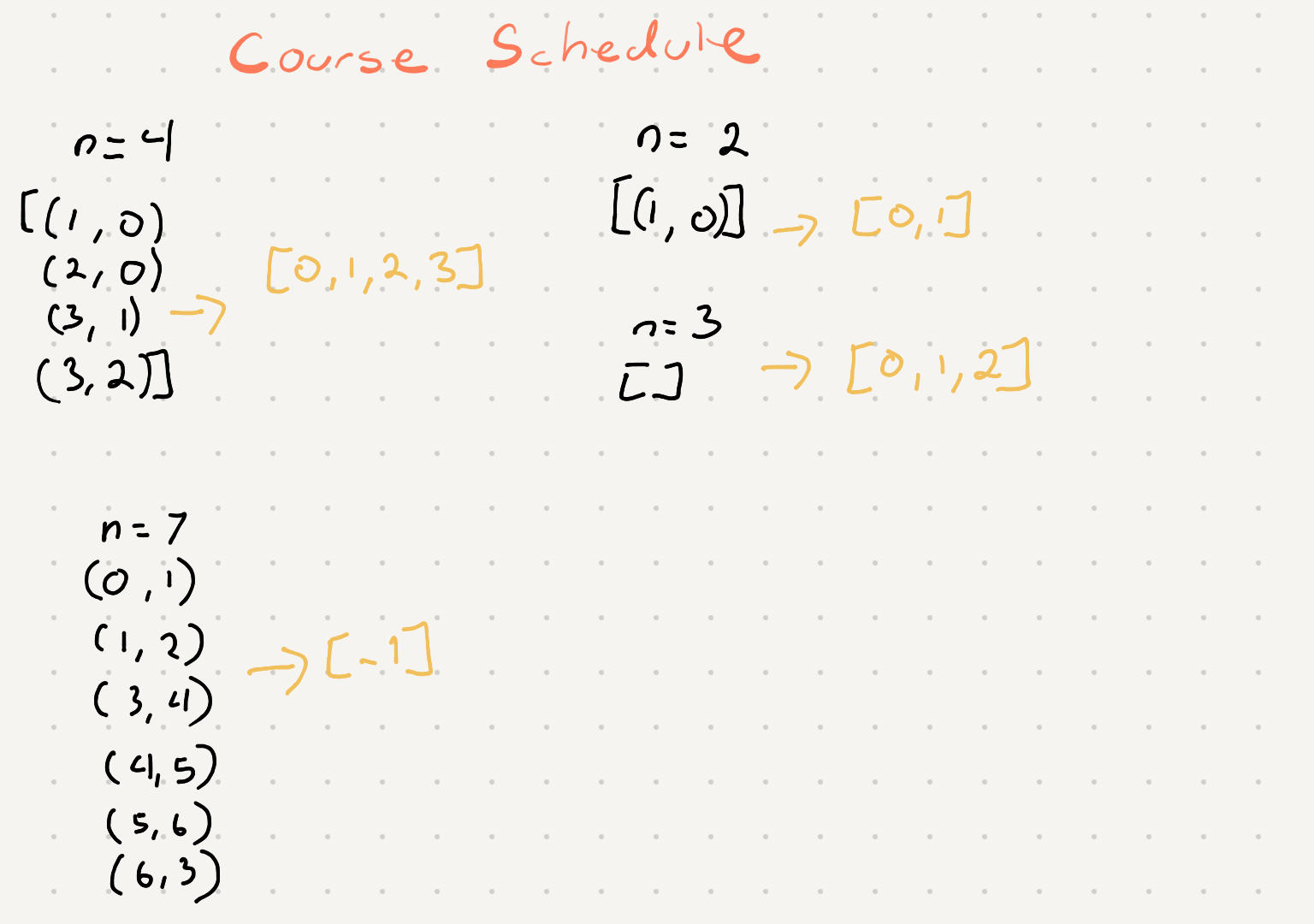
If we take a look at the prerequisite and were to draw out the connections between a course and it’s dependents it would look something like this

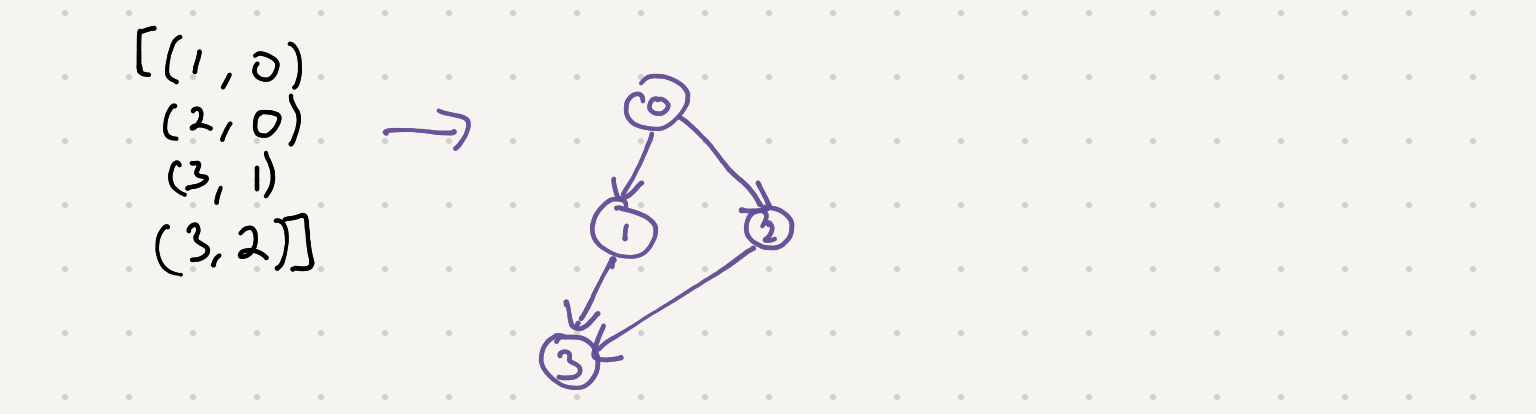
Looks pretty close to a graph right? So now we can think of our different algorithms for traversing a graph. Since we have to generate a schedule and make sure all the pre requisites come first we should opt for a DFS approach. This way we keep going down the chain of dependencies until we hit the very last one. Once we do hit that “leaf” node that doesn’t have any more dependencies we can assume it’s safe to add it to our schedule/path. Let’s recall our the standard DFS algorithm code -

def dfs(list_of_vertices):
    visited = set()

    for v in list_of_vertices:
        if v not in visited:
            explore(v, visited)

def explore(node, visited):
    visited.add(node)

    for v in node.neighbors:
        if (n not in seen):
            explore(v, visited)

So let’s example our problem again and see how we can change this standard algorithm to generate the schedule.

1. We need a way to keep appending to the path so we can return that path as our schedule.
2. We have to build a way to return all the dependencies of a course. One way we can do this is to build a table of all the prerequisites for a course and just do a lookup for our get_neighbors function
3. What happens when we encounter a situation where we have a circular dependency?
4. Consider the cases where no prereq information is given and we need to generate the rest of the schedule based on n

We can keep list to store the path to solve item #1

To me #3 was difficult to initially solve. We can’t just use our seen variable because a course could have multiple references as a pre requisite.

What exactly is a cycle in the case of a DFS algorithm. All it really means is that a node we’ve seen before got added to the call stack. Once that is allowed to happened wwe will have an infinite recursion because we’ll eventually keep adding the same node over and over. So if we can capture that first time we add a node back into our call stack we can determine that we have a cycle!

One thing we can do is keep track of a node and see if it’s in the call stack. We can label the node as VISITING and if we ever encounter that node again in the VISTING state we know the graph has a cycle.

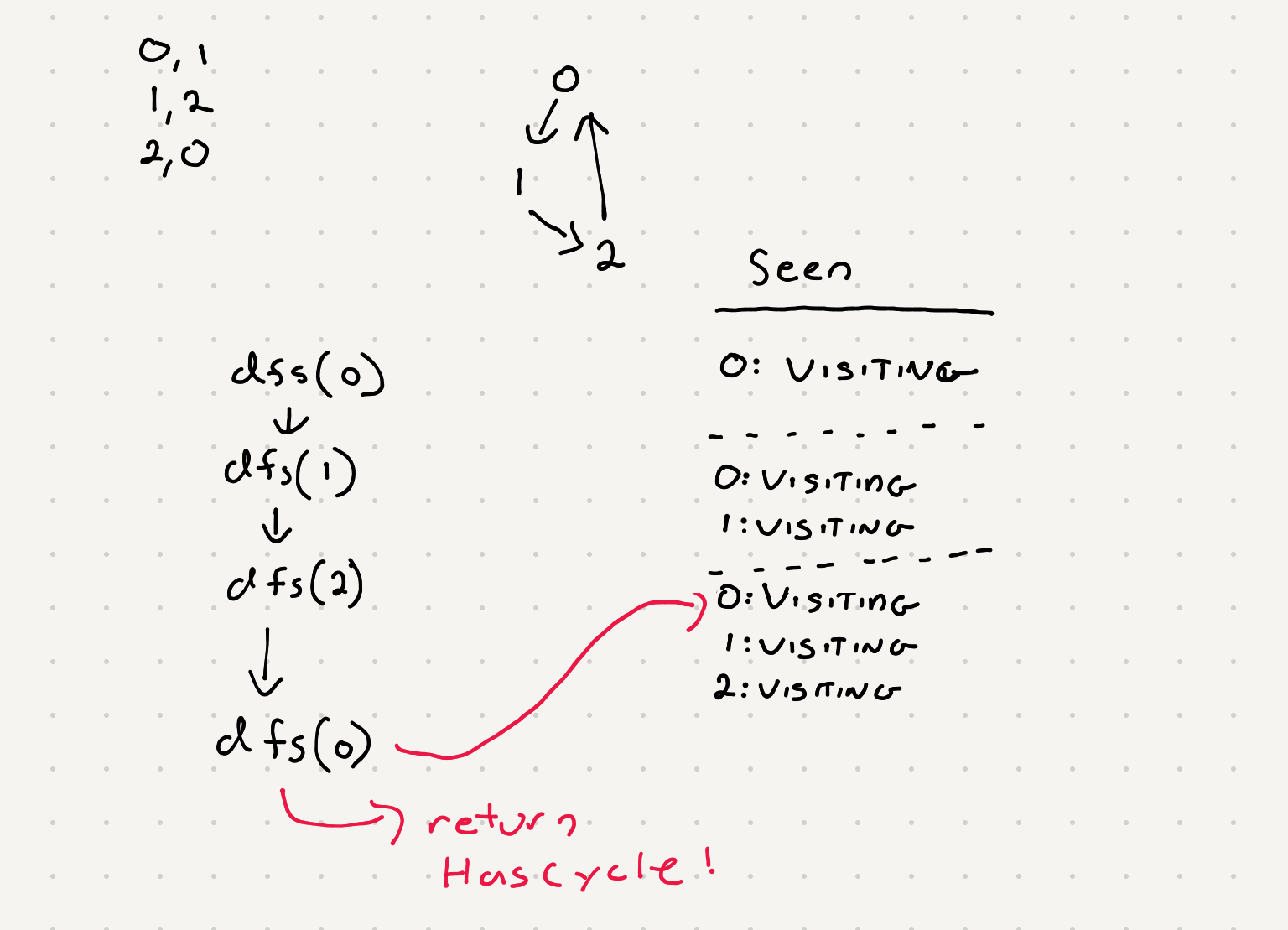
Let’s also go through an example where this is no cycle. Once we finished a dependency path we can mark those nodes as visited.

Putting 1,2,3 and 4 together we have

VISITED = 1
VISITING = -1

def gen_dep_list(prerequisites):
    # iterate through all values including prereq 
    # if we don't do this the prereqs that don't have any
    # prereqs would trigger a keyerror in the table lookup  
    table = {}

    for c, r in prerequisites:
        if c not in table:
            table[c] = set()
        
        if r not in table:
            table[r] = set()
    
        table[c].add(r)
            
    return table
    
def course_schedule(n, prerequisites):
    def dfs(course):
        if course in seen_and_status:
            if seen_and_status[course] == VISITING:
                has_cycle[0] = True

            return

        seen_and_status[course] = VISITING
    
        for required_course in table[course]:
            dfs(required_course)
            
        schedule.append(course)
        seen_and_status[course] = VISITED
    
    # no prereqs given so generate a schedule with n courses
    if not prerequisites:
        return list(range(n))
    
    table = gen_dep_list(prerequisites)
    seen_and_status = {}
    schedule = []
    has_cycle = [False]    # in a list container so we can pass by ref
    
    for course, _ in prerequisites:
        dfs(course)
    
    if not schedule or has_cycle[0]:
        return [-1]

    if len(schedule) < n:
        schedule += list(range(len(schedule), n))
        
    return schedule

The runtime of this will be O(v+e)