Count number of islands in a grid

Problem statement

Count the number of islands in 2 dimensional array. An island is denoted by the number 1 (land) and is surrounded by 0 (water). You can traverse up, down, left and right

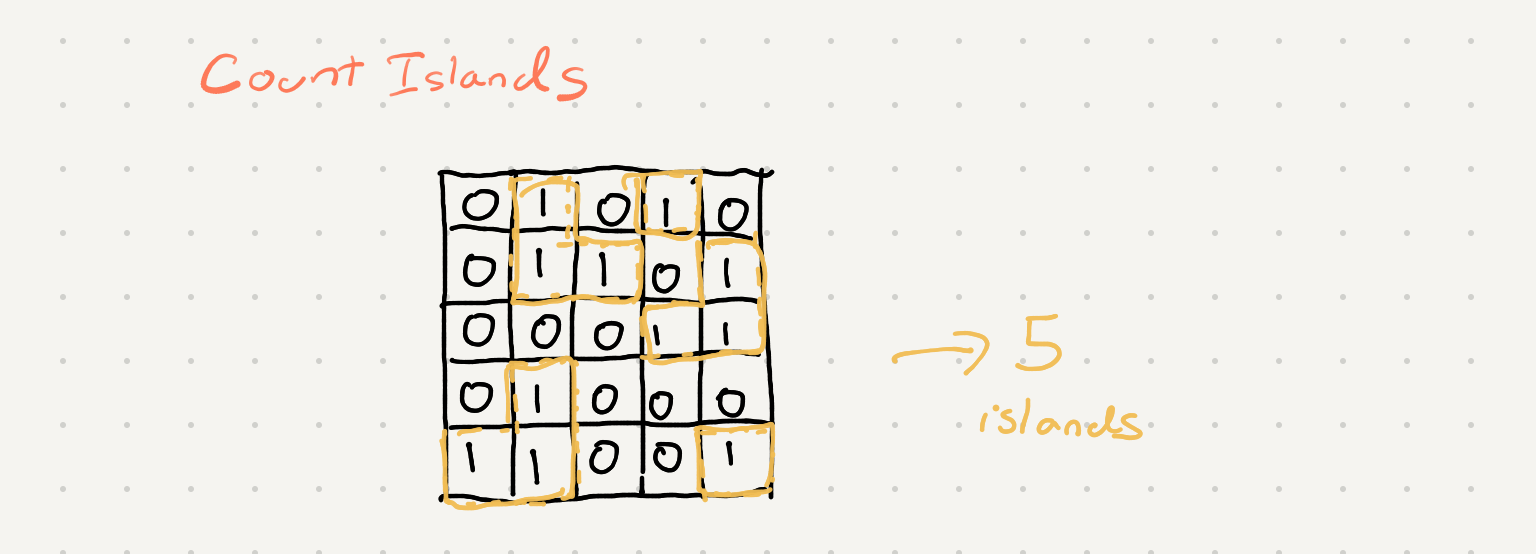
When looking at the input grid I initially thought we could solve this problem by keeping track of all the land in a row and iterating through all the rows and “joining” the islands. This seemed really complicated. The problem is is a bit simplified if you consider the grid as a set of connected nodes in a graph.

Take a look at the first island and all of it’s neighbors. We can traverse up down and left

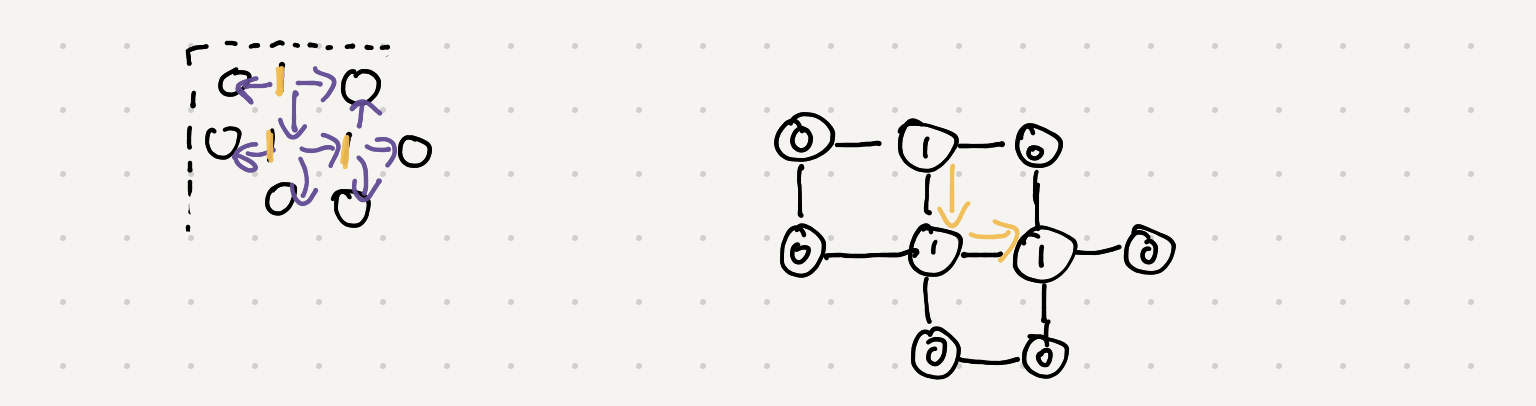
Instead of figuring out how to join all the data from the different rows let’s just do a graph traversal when we see the island and follow/map it out.

Recall the standard graph DFS algorithm

def dfs(list_of_vertices):
    seen = set()

    for cur in list_of_vertices:
        if (cur.val not in seen):
            path = []
            explore(cur, seen, path)
            print(path)

def explore(cur, seen, path):
    seen.add(cur.val)
    path.add(cur.val))

    for (n in cur.neighbors):
        if (n not in seen):
            explore(n, seen, path)

We’ll need to adapt this in a few different ways -

1. seen needs to not just be a set but a 2d array to make sure we don’t keep visiting the same nodes

2. our list_of_vertices needs to be all the list items so we’ll have to 2 for loops to iterate through each row and column.

3. Since we really only care about visiting island nodes we can ignore any nodes that are not 1

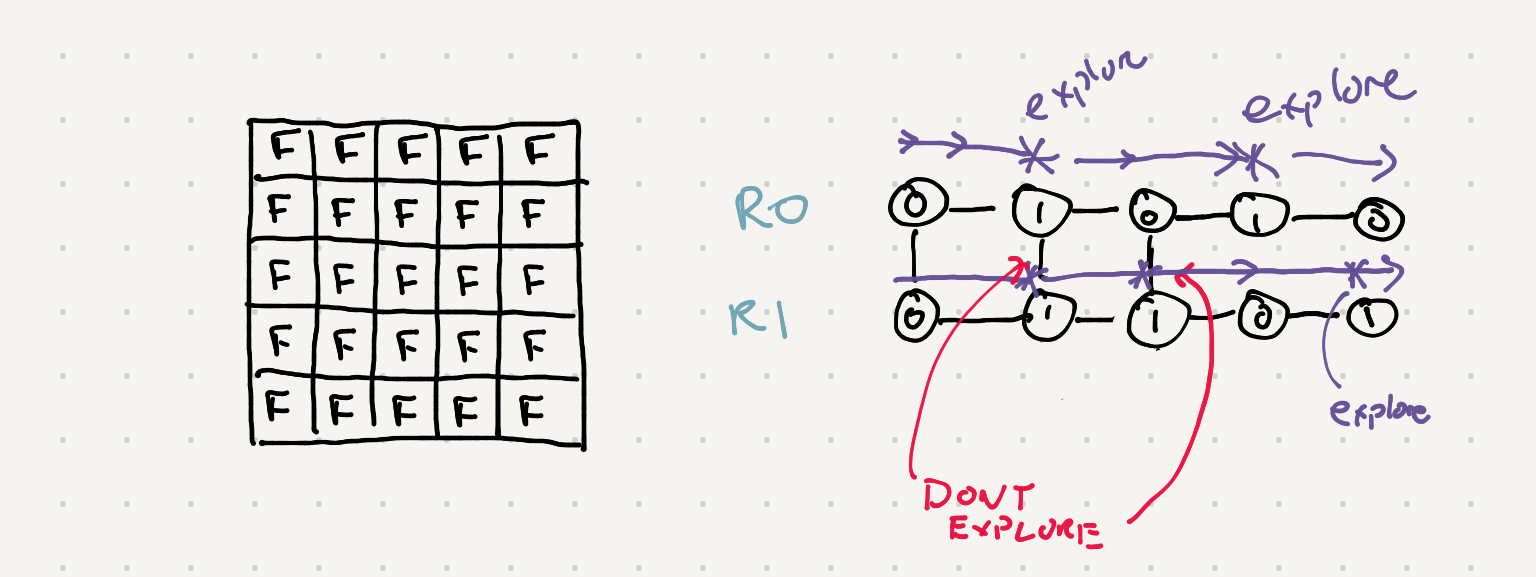
As we explore some land we mark all the connected lands as visited. That way the next time we iterate to future islands we can skip over them.

def dfs(grid):
    row_length, col_length = len(grid), len(grid[0])
    visited = [[False * col_length] * row_length]

    for row in range(row_length):
        for col in range(col_length):
            if (grid[row][col] == 1) and (not visited[row][col]):
                _explore(row, col)

    def _explore(row, col):
        if visited[row][col]:
            return

        visited[row][col] = True
        
        # TODO implement a function get_neighbors 
        for new_r, new_c in get_neighbors(row, col):
            if (grid[new_r][new_c] == 1) and (not visited[new_r][new_c]):
                explore(new_r, new_c)

Let’s take a look at how our seen table is filled up as we traverse our graph

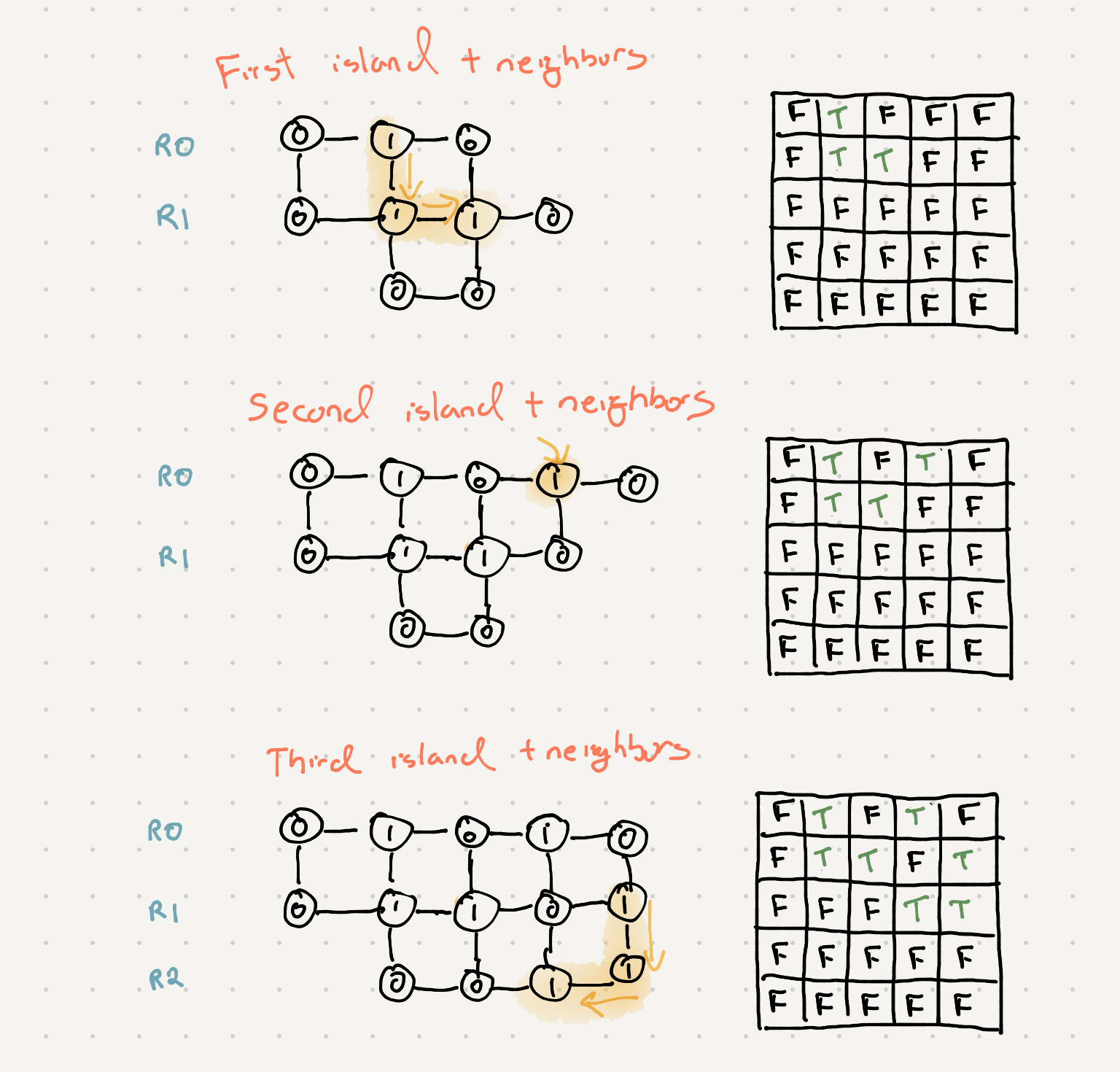
As you can see our table is filling up with all the areas that have islands. Since we know we will never visit an island again we can keep a variable that we increment before we start recursing through the grid.

The last bit to figure out is how to get all of a nodes neighbors. In our case we don’t have a neighbors variable on each node that we can iterate.

You can do the addition/subtraction of the current coordinates and validate if the new coordinate is on the grid.

One clean way I’ve seen people do this is to keep a list of directions from the 0,0 index and just add those values to where every you are on the grid.

Putting it all together we have

def dfs(grid):
    row_length, col_length = len(grid), len(grid[0])
    visited = [[False * col_length] * row_length]

    count = 0

    for row in range(row_length):
        for col in range(col_length):
            if (grid[row][col] == 1) and (not visited[row][col]):
                count += 1
                _explore(row, col)

    return count

    def _explore(row, col):
        if visited[row][col]:
            return

        visited[row][col] = True
        
        for new_r, new_c in get_neighbors(row, col):
            if (grid[new_r][new_c] == 1) and (not visited[new_r][new_c]):
                _explore(new_r, new_c)


    def _get_neighbors(r, c):
        DIRECTIONS = [(0, 1), (0, -1), (1, 0), (-1, 0)]

        valid_n = []

        for dir_r, dir_c in DIRECTIONS:
           new_r = r + dir_r 
           new_c = c + dir_c

           if (0 <= new_r < row_length) and (0 <= new_c < col_length):
            valid_n.append((new_r, new_c))
        
        return valid_n

The runtime for this graph would be O(V+E)