Clone a connected graph

Problem statement

Given a node in a connected graph clone the entire graph included the connection details

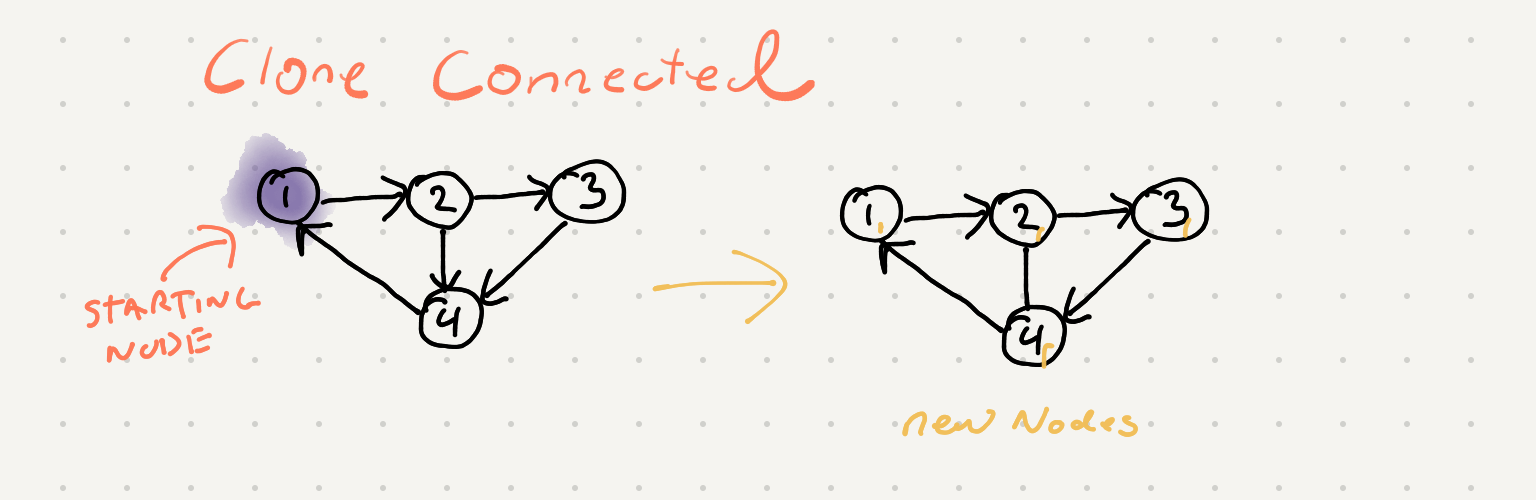
At first glance this problem seems pretty straight forward. We can just do a traversal and clone all the Nodes. While this would get us all the Nodes all the neighbor info wouldn’t be maintained. For example take a look at Node(4) who’s in the neighbor list for both Node(2) and Node(3). If we just simply traverse we won’t maintain that connection between Node(2) and Node(3).

So let’s take a look at a standard dfs approach to traversing the graph.

def dfs(list_of_vertices):
    seen = set()

    for cur in list_of_vertices:
        if (cur.val not in seen):
            path = []
            explore(cur, seen, path)
            print(path)

def explore(cur, seen, path):
    seen.add(cur.val)
    path.add(cur.val))

    for (n in cur.neighbors):
        if (n not in seen):
            explore(n, seen, path)

Since we are know that 1. the graph is connected and 2. only given one node we can rewrite the above

def explore_runner(start):
    seen = set()
    explore(start, seen)

def explore(start, seen):
    if start in seen:
        return

    for n in start.neighbors:
        if (n not in seen):
            explore(n, seen)

So to reiterate the earlier point about the connections not being minted if we just traverse let’s take a look at all the info at once.

node  |  neighbors
1        [2] 
2        [3,4]
3        [4]
4        [1]

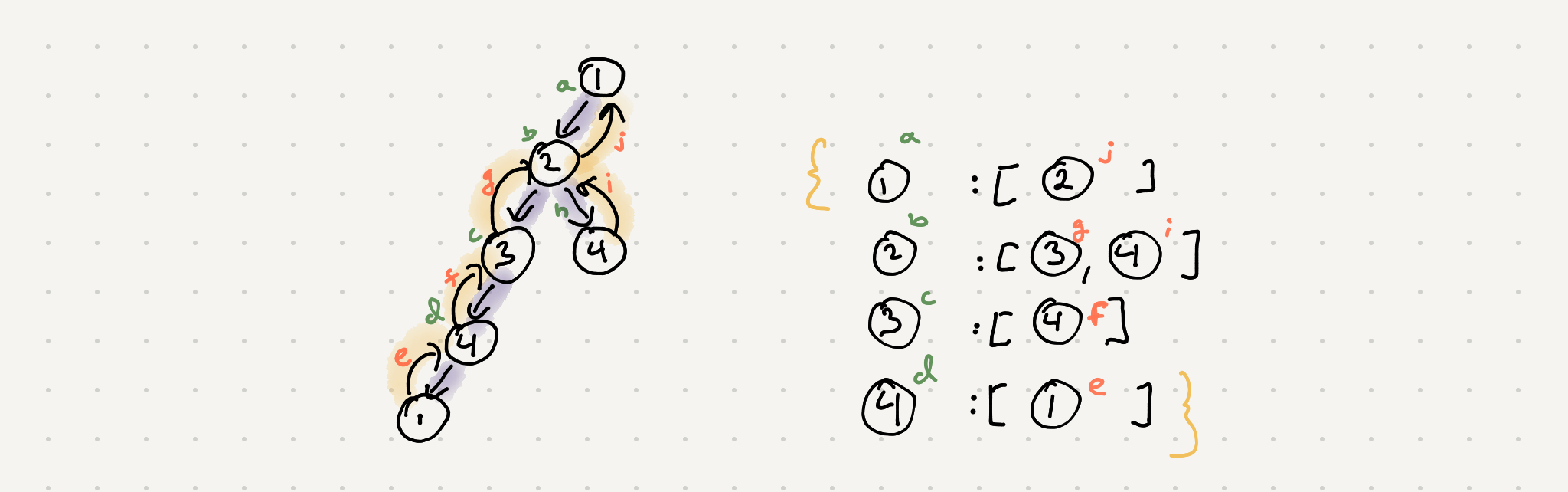
If we take a look at our explore function we see that we actually visit every neighbor of a node. We just immediately return if it’s in the seen set. What if we didn’t return none and return the neighbor object itself. If we did that we can assign it to the current clone of the node we are exploring. We can replace our set with a dictionary that can store the list of neighbors.

a. We look at Node(1) and fill in our map we then go to all of it’s neighbors
b. When traversing the neighbor we end up at Node(2)
c. When traversing the neighbors of Node(2) recurse w/Node(3)
d. When traversing the neighbors of Node(3) recurse w/Node(4)
d. When traversing the neighbors of Node(4) recurse w/Node(1)
e. Now at this point we have seen Node(1) already so we returned the actual Node(1) itself so we can append it to the neighbors list
f. Recurse back up the callstack since there are no more neighbors with the cloned object Node(4) and append it to Node(3) neighbor list
g. Recurse back up the callstack since there are no more neighbors with the cloned object Node(3) and append it to Node(2) neighbor list
h. When traversing the neighbors of Node(2) recurse w/Node(4)
i. Now at this point we have seen Node(4) already so we returned the actual Node(4)
j. Recurse back up the callstack since there are no more neighbors with the cloned object Node(4) and append it to Node(2) neighbor list
j. Recurse back up the callstack since there are no more neighbors with the cloned object Node(2) and append it to Node(1) neighbor list

Finally we return Node(1)

Putting it altogether

def clone_runner(node):
    clone_map = {}
    return clone(node, clone_map)

def clone(cur, clone_map):
    if cur.val in clone_map:
        return clone_map[cur.val]

    cloned = Node(cur.val)
    clone_map[cloned.val] = cloned

    for n in cur.neighbors:
        cloned_neighbor = clone(n, clone_map)
        clone.neighbors.append(cloned_neighbor)

    return clone

The runtime complexity of those will be O(v + e)