Least common ancestor of a Binary Tree

Problem statement

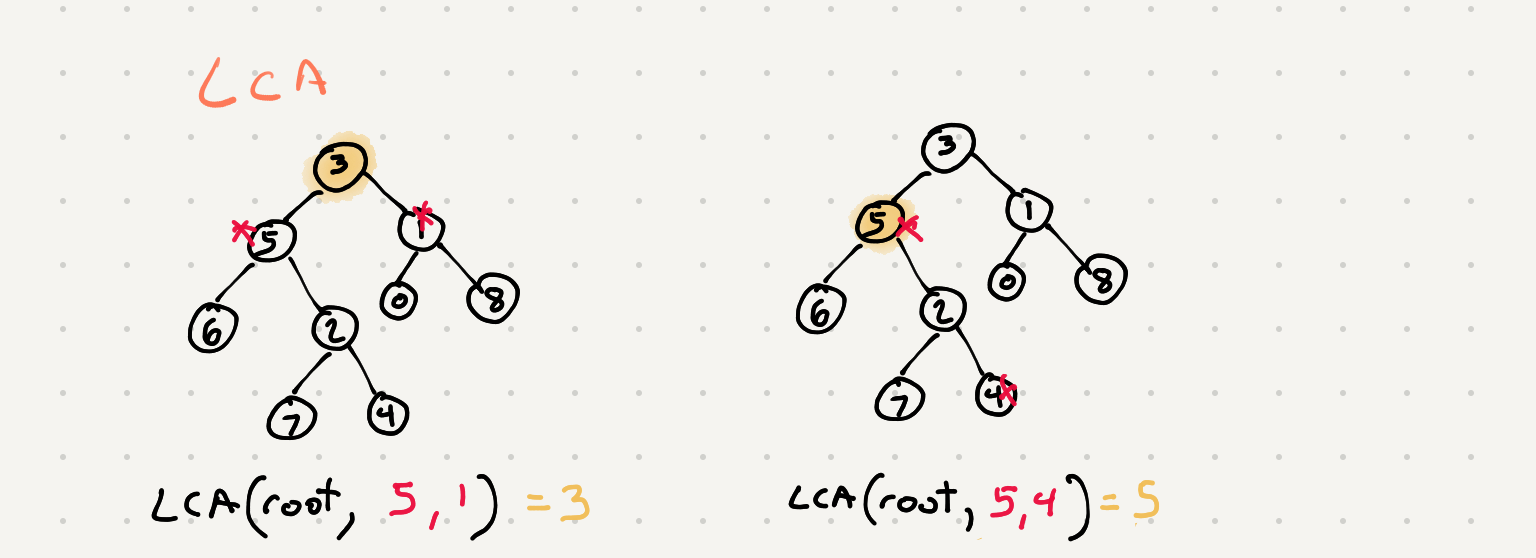
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

All of the nodes' values will be unique. p and q are different and both values will exist in the binary tree.

problem

So before we try to figure out the LCA let’s try to just solve the problem of finding a path to one of our targets. We can use a dfs algorithm and a seen array to track the path

def dfs_path(root, target, path_so_far):
    if not root:
        return True

    path_so_far.append(root)

    if root.val == target:
        return True
    
    left_found = dfs_path(root.left, target, path_so_far)
    right_found = dfs_path(root.right, target, path_so_far)

    if left_found or right_found:
        return True
    
    # case where we couldn't find the target so we remove elements from the path
    path_so_far.pop()
    return False

Let’s take a look at how this finds our target and keeps the path array updated with the right values

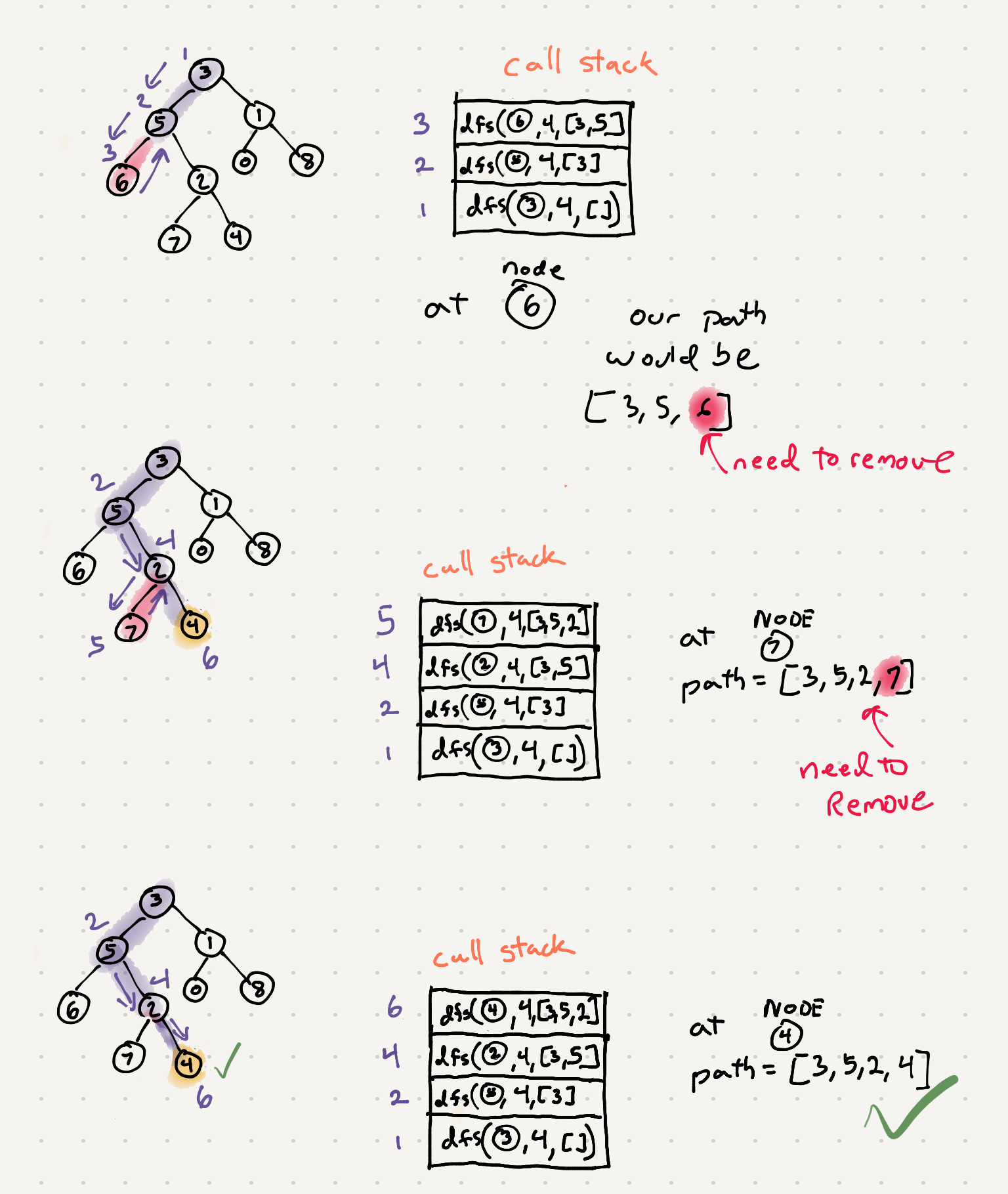
problem

So we can run this on both our targets. Once we have the paths to our targets. We now just iterate through both these paths until we get to a point where their paths are different. Once we hit that case we know that that’s the point their paths diverge.

problem

And putting it all together we have:

def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
    def dfs_path(root, target, path_so_far):
        if not root:
            return True

        path_so_far.append(root)

        if root.val == target:
            return True
        
        left_found = dfs_path(root.left, target, path_so_far)
        right_found = dfs_path(root.right, target, path_so_far)

        if left_found or right_found:
            return True
        
        # couldn't find the target so we remove elements from the path
        path_so_far.pop()
        return False

    def compare_paths(path_p, path_q):
        i = j = 0

        while i < len(path_p) and j < len(path_q):
            if path_p[i].val == path_q[j].val:
                i+=1
                j+=1
            else:
                break

        return path_p[i-1]
    
    # driver code -------------------------
    path_p = path_q = []

    dfs_path(root, p.val, path_p)
    dfs_path(root, q.val, path_q)

    return compare_paths(path_p, path_q)