Is it a BST?

Problem statement

Given a Binary Tree, check if it is a Binary Search Tree (BST). A valid BST doesn’t have to be complete or balanced.

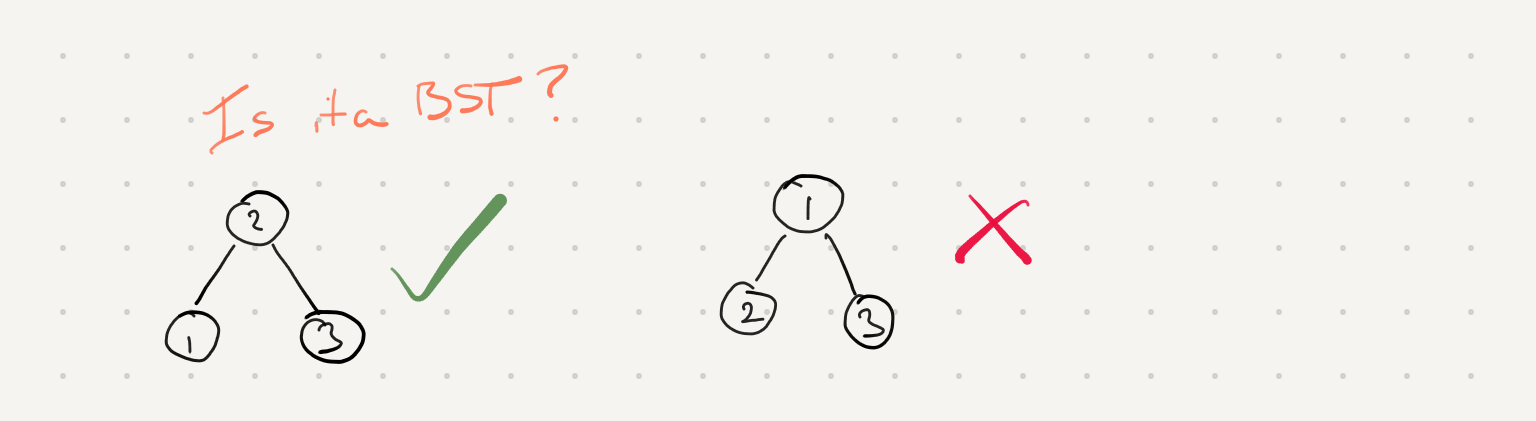
So we know one of the fundamental properties of a BST is that the value of the nodes on the left are less than the root and the ones on the right are greater then the root. So we have a bound to check against for the subtree on the left and the right.

We are going to traverse the entire tree to find out if every node is valid. So lets plan on doing a dfs traversal through the tree

So when visiting a node we need to make sure that on the left side we do a check like so to cause us to fail our is bst condition

if (val at the current root > maxiumum from above):
    return False

On the right side we need to make sure the values are larger than the root.

if (val at the current root < minimum value from above):
    return False

So when we start our traversal we need to use sufficiently large and small numbers for our min and max values. We will take the python systems min and max size for ints for this.

Lets walk through the recursion tree and see how our range changes as we traverse through.

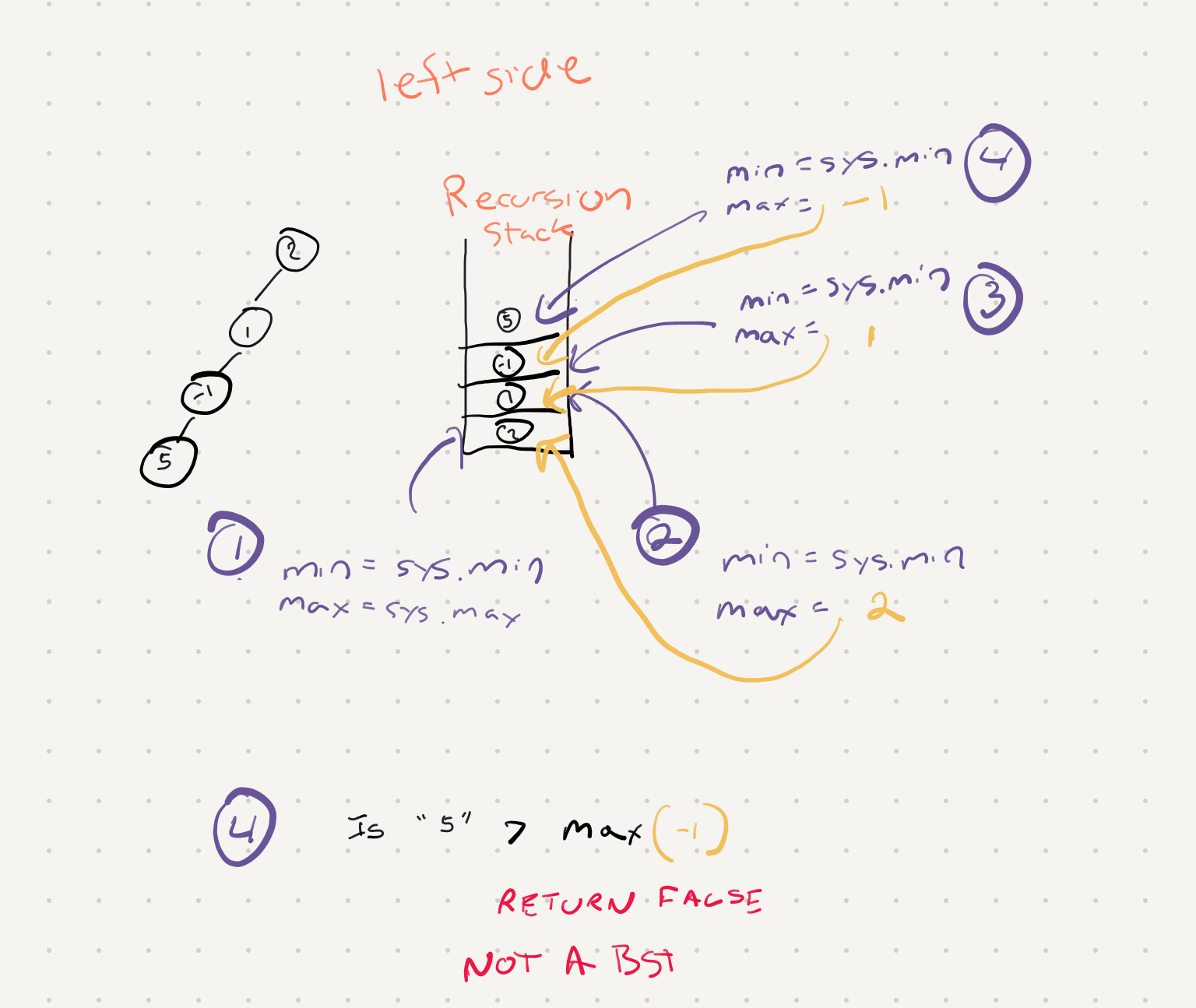So notice as we go further down the tree we change the max value to the value from the node above.

Now on the right side of things however we need to change both min and max values. Remember everything below a node on the left side has to be smaller then the root. So our range is different once we traverse a bit further down and look at the right side.

Lets go through the same example but at a different point and with a right node in the tree.

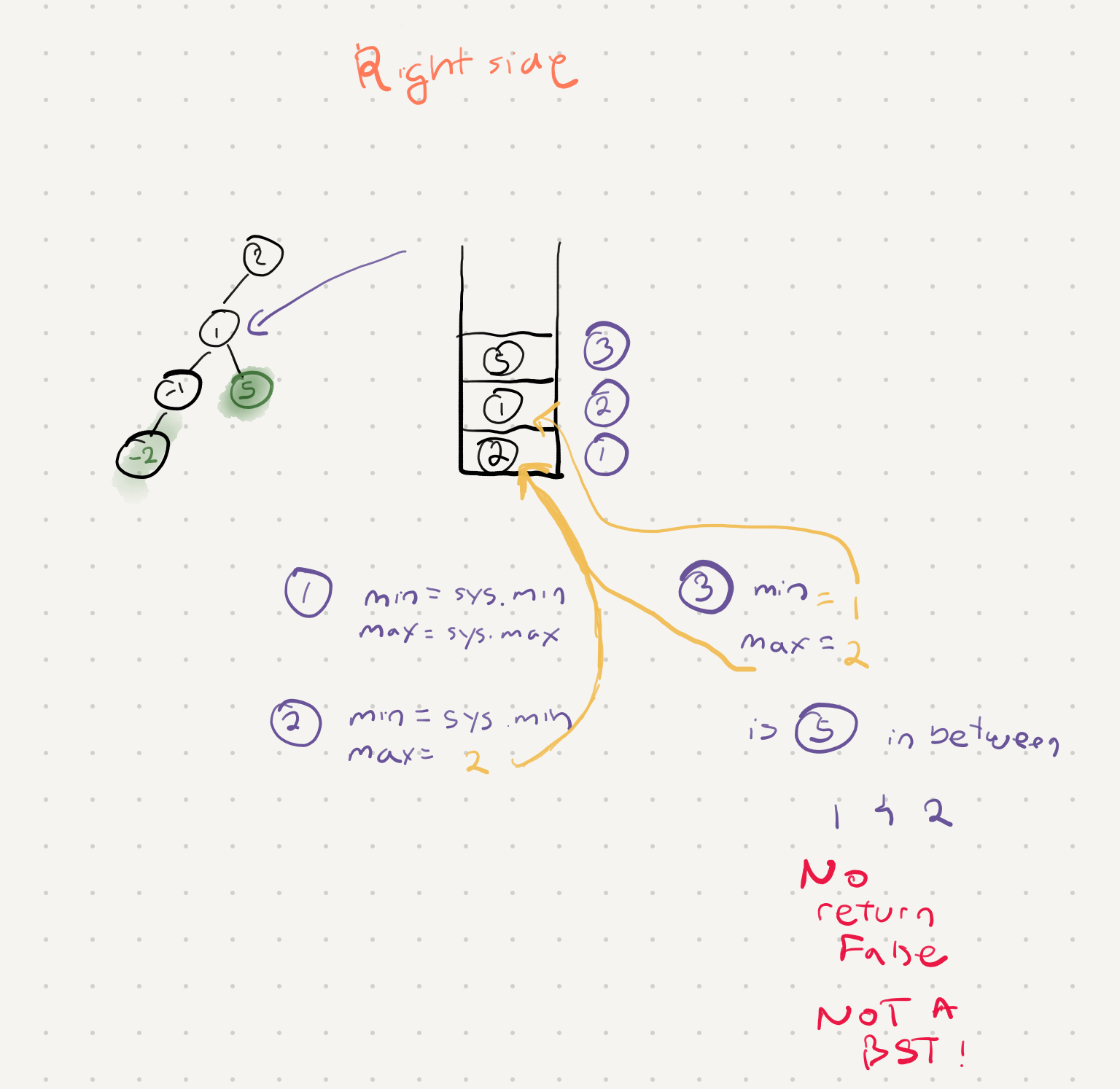
Putting it all together -

def isBSTInRange(root, minVal, maxVal):
    if not root:
        return True
    
    if (root.val > maxVal) or (root.val < minVal):
        return False
        
    left = isBSTInRange(root.left_ptr, minVal, root.val)
    right = isBSTInRange(root.right_ptr, root.val, maxVal)
    
    return left and right
    
def isBST(root):
    if not root:
        return True
        
    maxVal = sys.maxsize # => 9223372036854775807
    minVal = -sys.maxsize
    
    return isBSTInRange(root, minVal, maxVal)

The time complexity of this solution will be O(n) since we need to traverse every node to make sure it’s within a range.