Single Value / Unival tree

Problem Statement:

Given a binary tree, find the number of unival subtrees (the unival tree is a tree which has the same value for every node in it).

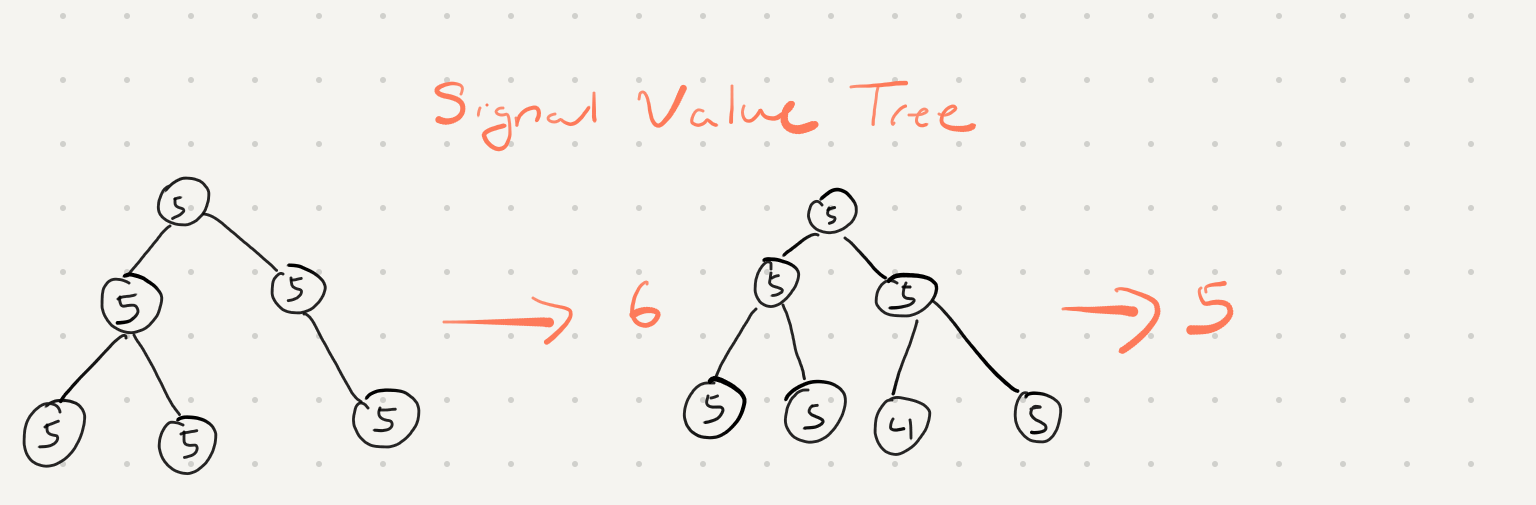
problem

Let’s break down this problem into smaller subproblems.

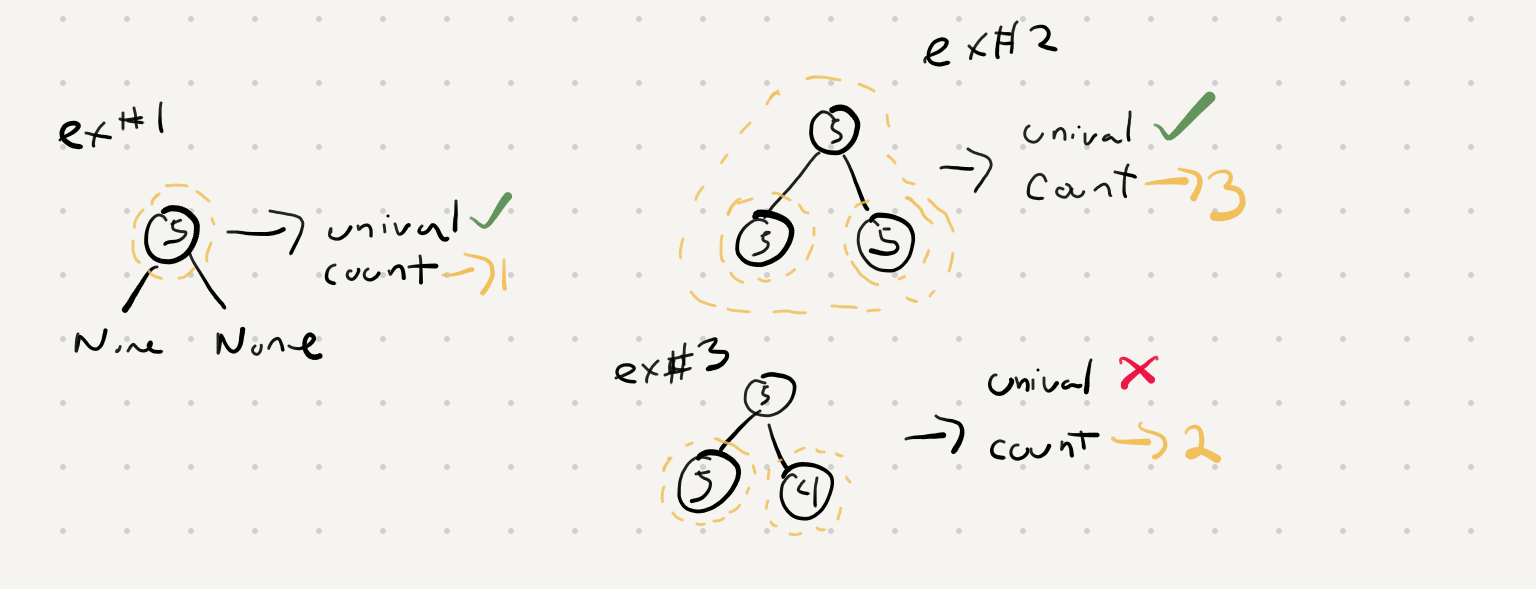
subproblem

ex.1 shows just one node. In this case all the nodes are the same so it’s a unival tree and the count is 1
ex.2 3 identical valued nodes should return 3 unival trees.
the two leaf nodes = 2 unival nodes
the whole tree itself is a unival so 2+1 = 3
ex.3 we see that one of the leaf nodes invalidates the “univalness” of the whole tree. It should still return 2 nodes because of the leaf nodes.

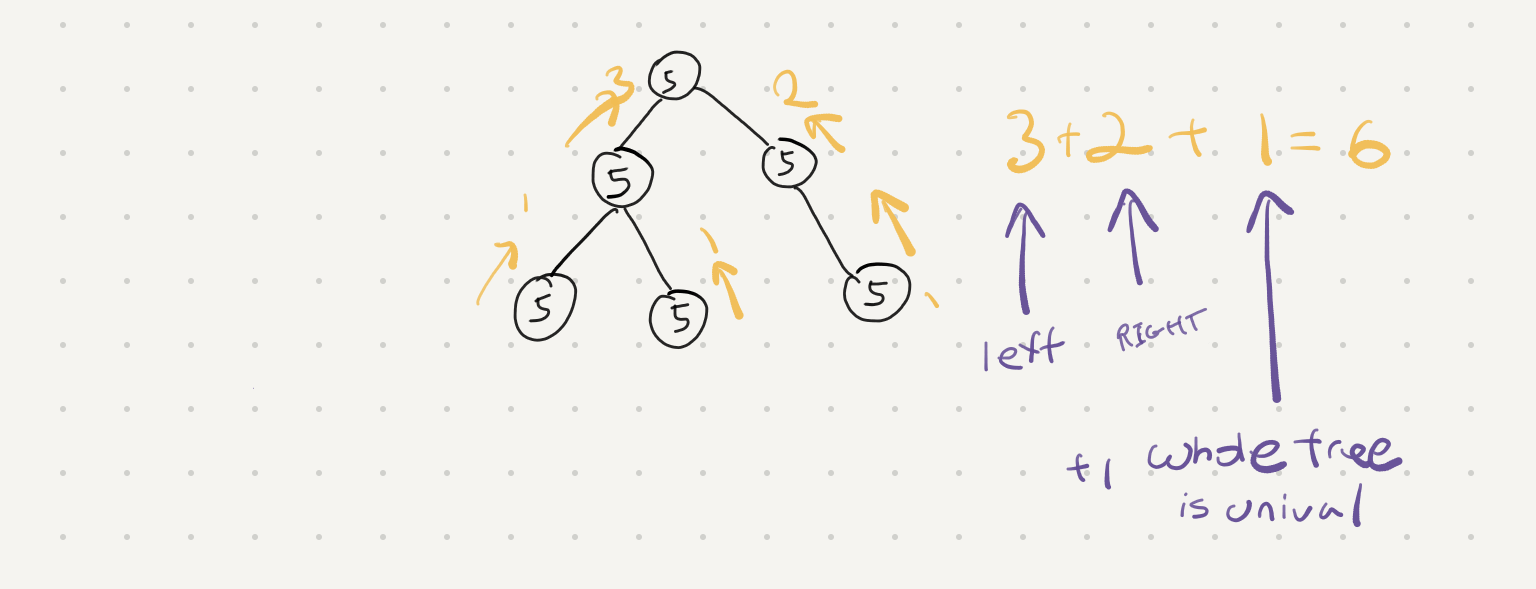
So we can see here we need to evaluate the values of the left and right nodes compared to the root node. We also have to do a number of unival nodes on the left and the right.

So working through our example we can create a formula for adding up all the counts

example

def unival_count(root):
    if root == None:
        return 0


    # check if a leaf node 
    if root.left_ptr == None and root.right_ptr == None:
        return 1
    
    count_left = unival_count(root.left_ptr)
    count_right = unival_count(root.right_ptr)
    total_count = count_left + count_right

    # compare the values of root to left and right
    if root.left_ptr and root.left_ptr.val != root.val:
        return total_count
    
    if root.right_ptr and root.right_ptr.val != root.val:
        return total_count

    # Both left and right are equal
    return total_count + 1

Doing it again for the second example reveals an edge case however

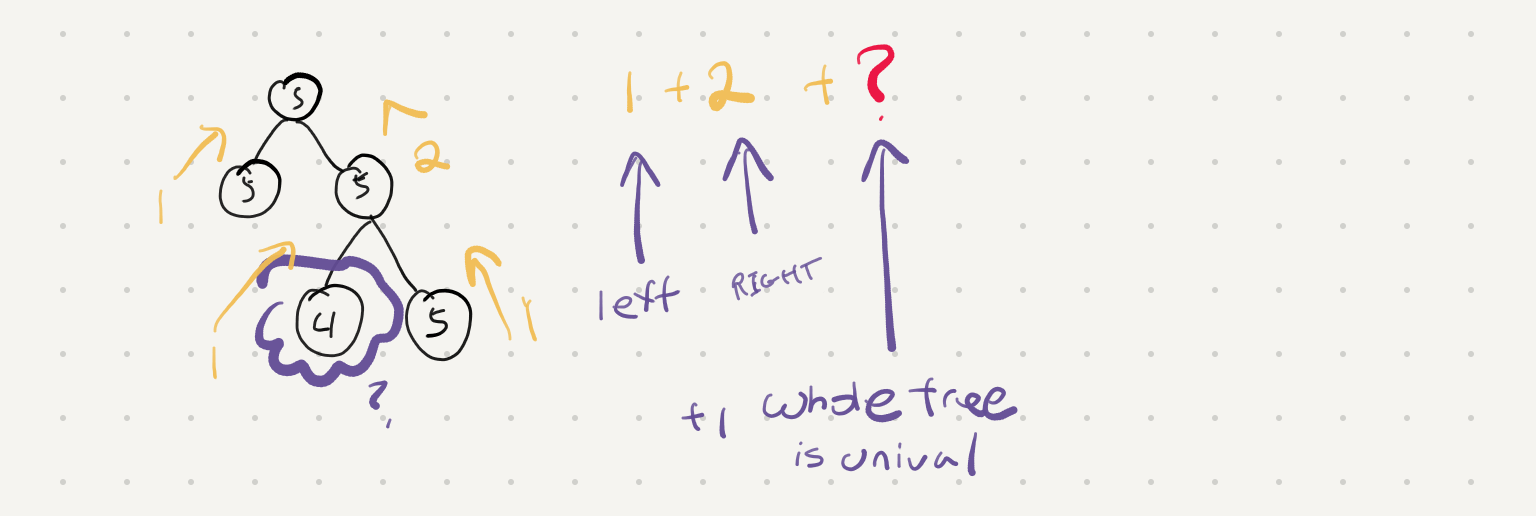
example2

We can get counts of the number of unival trees but we can’t evaluate the “univalness” of the whole tree. That leaf node of 4 should invalidate the whole tree and we need to pass that information on up the stack. We can do that by not just returning the total counts but also a boolean to let us know - hey was the subtree below us unival? If it was then we can keep returning true but if not we just bubble up that false value.

So our tweaked and final code will look something like this

def findSingleValueTrees(root):
    count, is_unival = unival_count(root)
    return count
    
def unival_count(root):
    if root == None:
        return 0, True
    
    if root.left_ptr == None and root.right_ptr == None:
        return 1, True
    
    count_left, is_unival_left = unival_count(root.left_ptr)
    count_right, is_unival_right = unival_count(root.right_ptr)
    total_count = count_left + count_right

    # if we have non unival trees in either side no point in 
    # adding that + 1 and return early! 
    if not is_unival_left or not is_unival_right:
        return total_count, False

    if root.left_ptr and root.left_ptr.val != root.val:
        return total_count, False
    
    if root.right_ptr and root.right_ptr.val != root.val:
        return total_count, False

    # Both left and right are equal          
    return total_count + 1, True