Binary Tree Maximum Path Sum

Problem Statement:

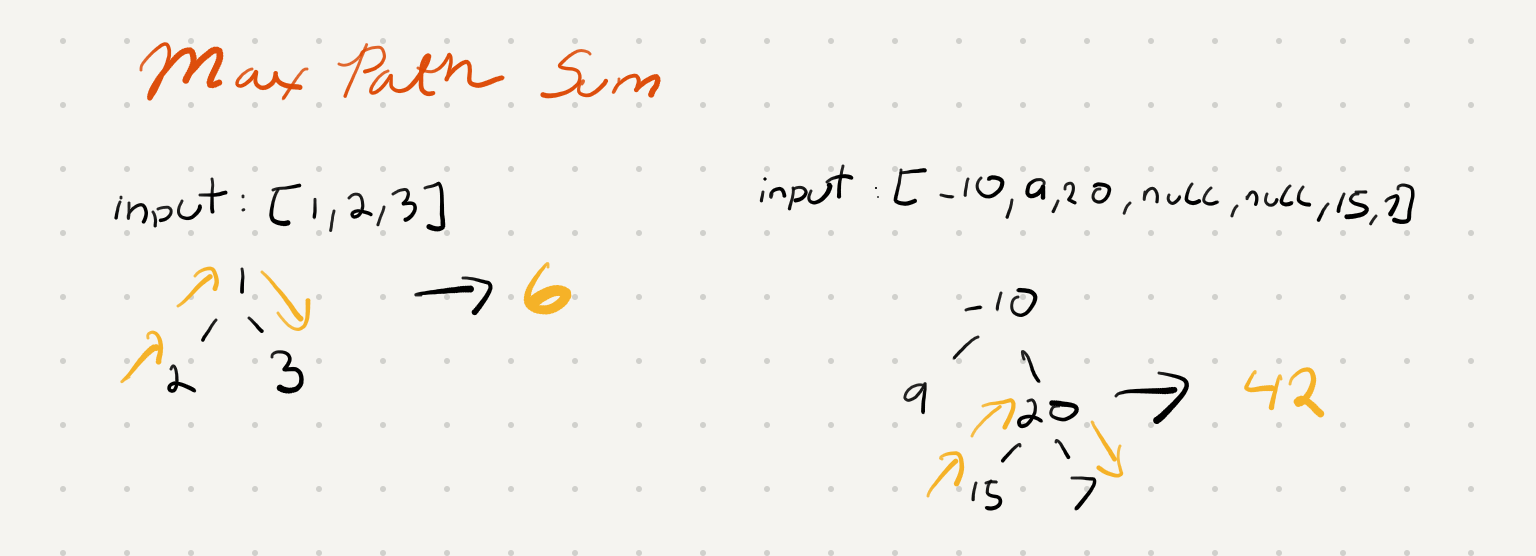
Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Similar to the other recursive tree problems we solved we need can try to solve this by solving the subproblems ie. the smaller trees.

If we try to use a DFS approach for the second example we can solve the max_path_sum of the nodes starting at 20. We can then use that result to evaluate our options when we return to the node at -10.

Lets walk through our cases

As you can see all our cases are actually lower then the path we could generate in the subtree starting at node 20. One way we can get around this is to keep a variable that tracks the maximum sum we have every come across (GLOBAL_MAX)

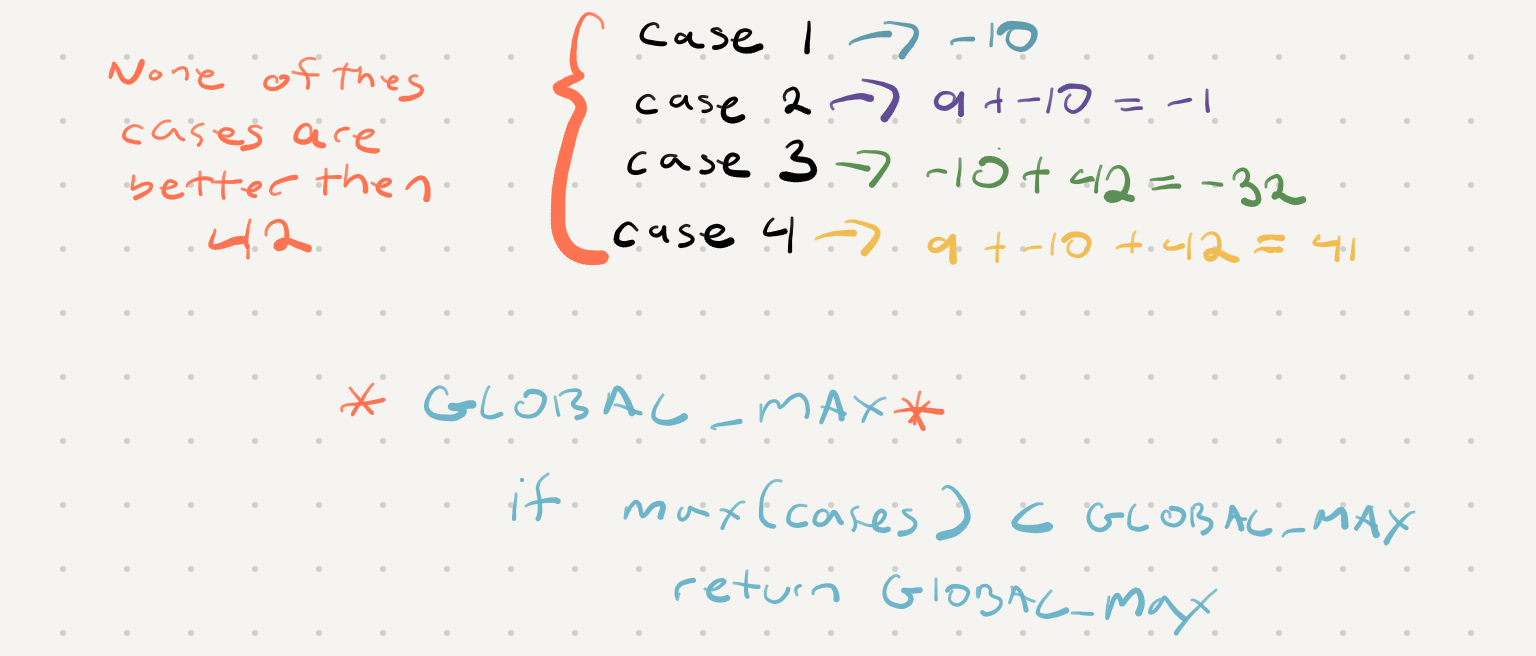
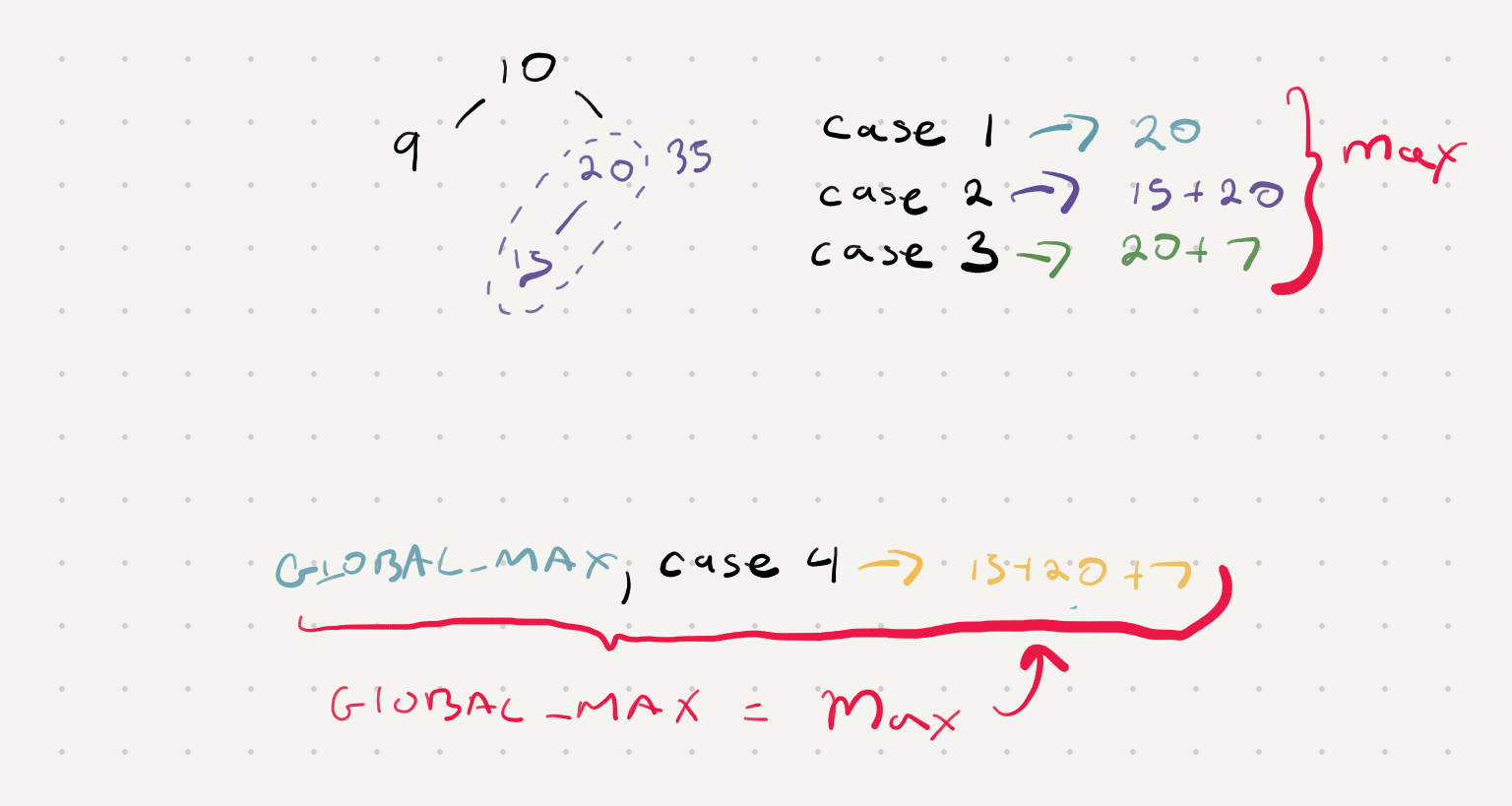
So this solves an edge case of having a subtree with a greater path. We have another edge case we should consider and that’s if we can generate a greater path through only one of the paths in the subtree.

So now we don’t just need the max seen but also which path is better left or right.

The solution here is to return the maximum of our 3 cases to the parent caller. We will use our fourth case to evaluate if we need to update our GLOBAL_MAX

def max_path_sum(root, g_max):
    if not root:
        return 0
    
    left = max_path_sum(root.left, g_max)
    right = max_path_sum(root.right, g_max)
    
    case_1 = root.val
    case_2 = left + root.val
    case_3 = root.val + right
    
    # update the global max 
    case_4 = left + root.val + right
    g_max[0] = max(g_max[0], case1, case2, case3, case_4)
    
    return max(case_1, case_2, case_3)
    
    
def runner(root):
    g_max = [0]
    val = max_path_sum(root, g_max)

    return max(g_max[0], val)